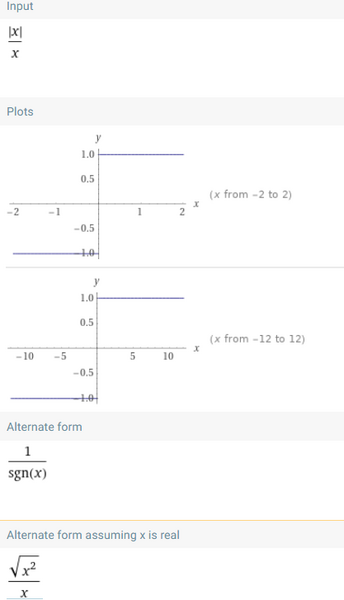
Esercizio 4. Data la funzione $f: R \backslash\{0\} \rightarrow R$ definita da $f(x)=\frac{|x|}{x}$, verificare che
$$
f(0-)=\lim _{x \rightarrow 0^{-}} \frac{|x|}{x}=-1
$$
$e$
$$
f(0+)=\lim _{x \rightarrow 0^{+}} \frac{|x|}{x}=+1
$$
Dire quindi se la funzione ammette limite per $x$ che tende a $0 .$ Risulta
$$
f(x)=\frac{|x|}{x}= \begin{cases}-1 & \text { if } x<0 \\ 1 & \text { if } x>0\end{cases}
$$
Facciamo vedere che $f(0-)=-1$. Fissato $\varepsilon>0$ consideriamo la disequazione
$$
|f(x)-(-1)|=|-1-(-1)|=0<\varepsilon
$$
che risulta banalmente soddisfatta per ogni $x<0$ quale che sia $\delta>0$. Concludiamo che $f(0-)=-1$.
Analogamente si verifica che $f(0+)=1$. Infine, essendo
$$
f(0-) \neq f(0+)
$$
possiamo dire che la funzione $f(x)=\frac{|x|}{x}$ non ammette limite per $x$ che tende a 0 .