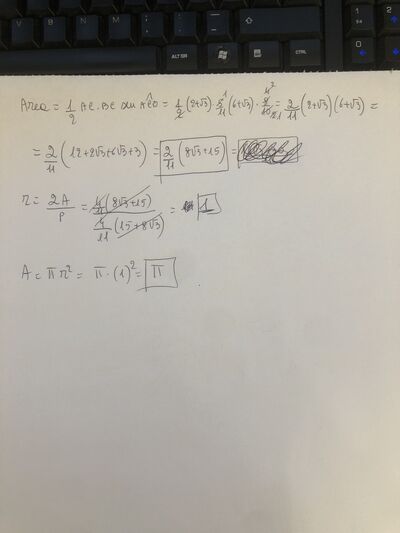Problemi di Trigonometria. Qualcuno riesce a risolvere questi esercizi e a spiegarmi il procedimento che ha usato per risolverli? Gli esercizi sono il 105-214-233.
105
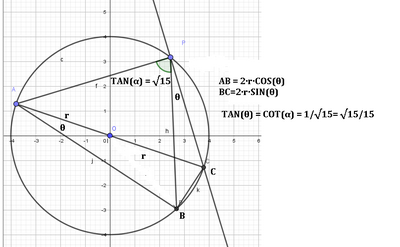
Due corde consecutive $A P$ e $P B$ di una circonferenza di raggio $r$ sono tali che $\tan A \widehat{P} B=\sqrt{15}$. Da $P \operatorname{traccia} l_2$ perpendicolare alla corda $A P$, indicando con $C$ l'ulteriore punto di intersezione di tale retta con la circonferenza, Determina $\overline{A B}+\overline{B C}$.
233
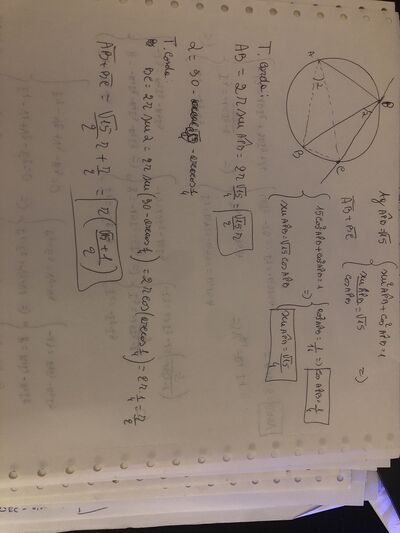
In un triangolo $A B C$ il lato $B C$ è doppio del lato $A B$. Sapendo che $\cos A \widehat{B C}=\frac{1}{4}$ e che il perimetro del triangolo è $10 \mathrm{~cm}$, determina le lunghezze dei lati del triangolo.
(Suggerimento: poni $\overline{A B}=x$ e imposta un'equazione, utilizzando il teorema del coseno.) $[A B=2 \mathrm{~cm} \mathrm{e} B C=A C=4 \mathrm{~cm}]$
214
In un triangolo un lato misura $2+\sqrt{3}$ e gli angoli a esso adiacenti sono l'uno di ampiezza $60^{\circ}$ e l'altro ha il seno uguale a 0,8 . Quanto vale l'area del cerchio inscritto nel triangolo?