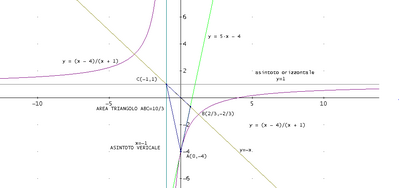
Data la curva di equazione $y=\frac{2 x-a}{b x+c}$, trova $a, b, c$, sapendo che ha per asintoto la retta $y=1 \mathrm{e}$ per tangente in $A(0 ;-4)$ la retta $t: y=5 x$ - 4. Considera poi la retta passante per il centro di simmetria Ce alla bisettrice del secondo e quarto quadrante, determinando la sua intersezione $B$ con la retta $t$. Calcola l'area
del triangolo $A B C$. $\left[a=8, b=2, c=2 ; B\left(\frac{2}{3} ;-\frac{2}{3}\right) ;\right.$ area $=1$
Buongiorno a tutti, volevo chiedere se qualcuno può aiutarmi con questo esercizio? (Se è possibile, potreste allegarmi una foto con il procedimento o una spiegazione ben dettagliata?)