esercizi con le coniche

Question

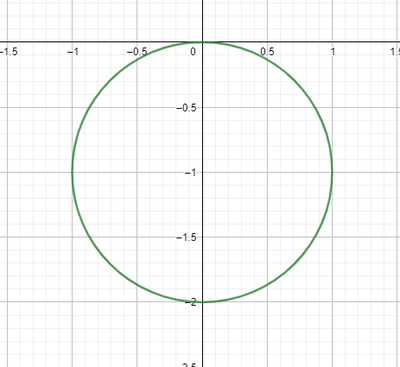
a. Nel fascio di curve di equazione (k+1)x^2+y^2-2kx+2y+k=0 individa per quale valore di k si ottiene una circonferenza e rappresentla graficamente indicado con O e A le sua intersezioni on gli assi cartesiani.

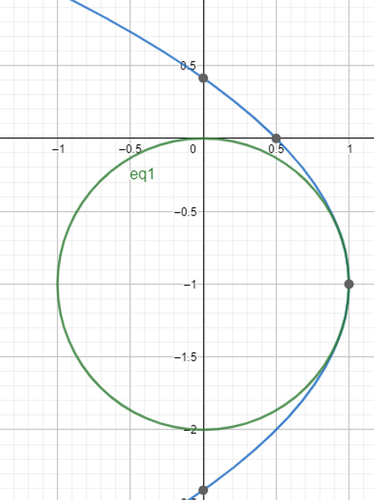
b. Studia la curva che si ottiene per k=1 e chiama B la sua intersezione con la circonferenza.

c. Stavilisci pe quali valori di k l'equaazione data rappresenta un'ellisse e in tal caso determinare il luogo dei entri L.

d. Determina il luogo L' simmetrico di L rispetto alla bisettrie del primo e terzo quadrante. Il luogo L' interseca la parabola nei punti C e D. Verifia che il triangolo BCD è simile al triangolo OAB e alcolarne il rapporto r di similitudine.

Autore

Risposta

Antonio22

(@antonio22)

6 punti

livello:

Livello 0

4 Risposte
3 0 1

28/05/2020 19:00

Sebastiano · Accepted Answer

a) per ottenere una circonferenza il coefficiente di $x^2$ deve essere pari a 1, quindi

$k+1=1$ da cui $k=0$.

l'eq. risulta:

$x^2+y^2+2y=0$

per k=-1 l'eq. diventa:

$y^2+2x+2y-1=0$ cioè $x=-y^2/2-y+1/2$ che rappresenta una parabola con asse parallelo all'asse delle x.

mettendo a sistema con la circonferenza esce:

$(-y^2/2-y+1/2)^2+y^2+2y=0$ che dopo avere esplicitato il quadrato diventa:

$y^4+4y^3+6y^2+4y+1=0$

si riconosce facilmente (triangolo di Tartaglia) che questo non è altro che

$(y+1)^4=0$ che ha 4 radici coincidenti in $y=-1$

corrispondentemente l'ascissa dell'unico punto di intersezione è $x=-1/2+1+1/2=1$

Il punto di intersezione (e di tangenza) è quindi $B(1,-1)$

c)per essere un'ellisse deve succedere che i coefficienti di $x^2$ e $y^2$ siano entrambi positivi (concordi) quindi $k+1>0$ da cui si ricava $k>-1$

Sebastiano

(@sebastiano)

16992 punti

livello:

Livello 9

3236 Risposte
7 818 1370

28/05/2020 19:04

[Risolto] esercizi con le coniche

Domande