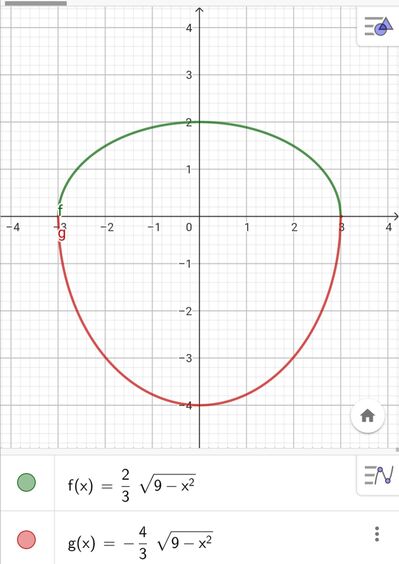
Considera le due funzioni $f(x)=\frac{2}{3} \sqrt{9-x^2}$ e $g(x)=-\frac{4}{3} \sqrt{9-x^2}$.
a. Traccia i grafici delle due funzioni.
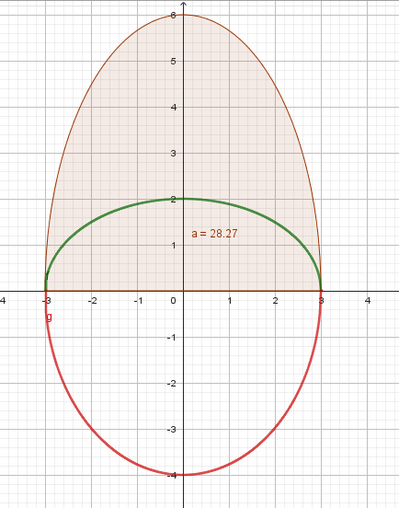
b. Determina l'area della regione di piano limitata dai grafici di fe di $g$.
Considera quindi la retta $r$ di equazione $x=t$ e rispondi ai seguenti ulteriori quesiti.
c. Determina per quali valori di $t$ la retta $r$ interseca sia il grafico di $f$ sia quello di $g$.
d. Nelle ipotesi di cui al punto precedente, indica con $P$ e $Q$, rispettivamente, i punti di intersezione della retta con i grafici di $f$ e di $g$, e determina per quali valori di $t$ risulta $\overline{P Q}=4$.
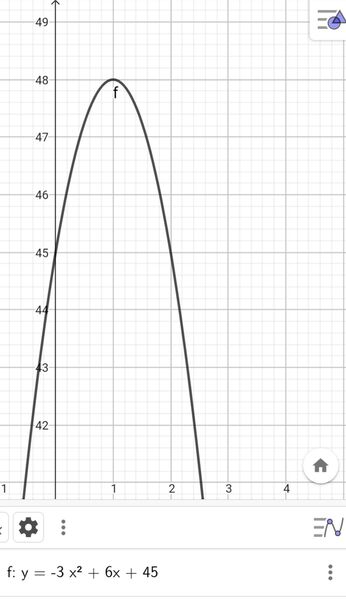
e. Indicata con $H$ la proiezione di $P$ sulla retta $x=-3$, determina l'espressione analitica della funzione: $z(t)=\overline{P H}^2+\overline{P Q}^2$
Determina infine il valore massimo di $z(t)$ e il valore di $t$ per cui si ottiene tale valore massimo.
Ciao a tutti avrei bisogno di sapere come svolgere questo esercizio.
grazie mille!