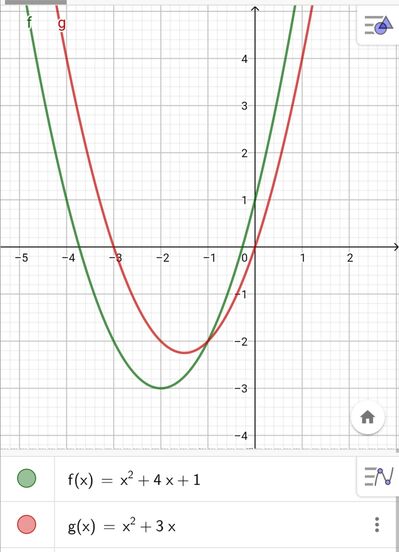
Il grafico rappresenta una funzione del tipo $y=a x^2+b|x|+c$. Trova $a, b, c$.
a. Nel fascio di rette di centro $A$ determina l'equazione della retta passante per il punto $B$ della curva di ascissa 5 e trova l'altro punto di intersezione $C$ della retta con il grafico.
b. Calcola la misura del segmento $B C$.
c. Sull'arco $\overparen{C A}$ della curva determina un punto $P$ in modo che $\sqrt{2} \overline{P Q}+\overline{P R}+\overline{P S}=\frac{5}{2}$, essendo $\overline{P Q}, \overline{P R}, \overline{P S}$ le distanze di $P$ rispettivamente dalla retta $A C$, dall'asse $x$ e dall'asse $y$.