L’espressione analitica che descrive una funzione può avere due forme:
- forma esplicita, del tipo
- forma implicita, del tipo
ESEMPI
Nel primo caso abbiamo (forma esplicita), nel secondo caso abbiamo
(forma implicita).
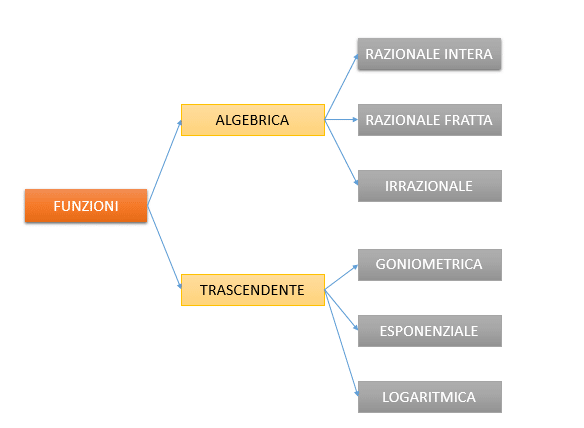
Se l’ espressione contiene soltanto operazioni di addizione, sottrazione, moltiplicazione, divisione, elevamento a potenza o estrazione di radice, la funzione è algebrica.
Una funzione algebrica in forma esplicita può essere:
- razionale intera (o polinomiale) se è espressa mediante un polinomio; in particolare, se il polinomio è di primo grado rispetto alla variabile x, la funzione si dice lineare, se il polinomio in x è di secondo grado, la funzione è detta quadratica;
- razionale fratta se è espressa mediante quozienti di polinomi;
- irrazionale se la variabile indipendente compare sotto il segno di radice.
ESEMPI
- Le funzioni
e
sono razionali intere. La prima è lineare, la seconda è quadratica.
- La funzione
è razionale fratta.
- La funzione
è irrazionale.
Se una funzione non è algebrica, si dice trascendente. Ad esempio, sono trascendenti tali funzioni: logaritmica, esponenziale e la funzione goniometrica.