DEFINIZIONE
Una relazione fra due insiemi A e B è una funzione se a ogni elemento di A associa uno e un solo elemento di B.
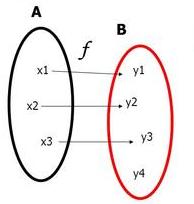
Poiché una funzione fa corrispondere a ogni elemento di A un unico elemento di B, essa viene anche chiamata corrispondenza biunivoca.
Per indicare una funzione si usa una lettera minuscola nel seguente modo:
che si legge: ” f è una funzione da A a B ”.
Si dice che A è l’insieme di partenza della funzione e B l’insieme di arrivo.
Si può utilizzare una notazione simile anche per indicare che a un elemento x di A corrisponde un elemento y di B : .
La y è detta l’immagine di x mediante la funzione f.
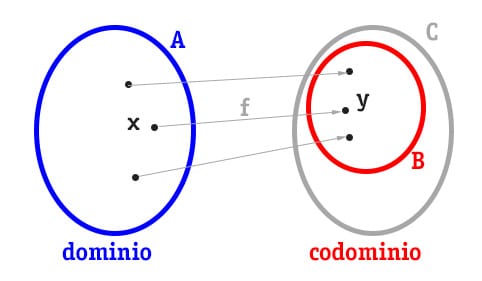
L’insieme di partenza A è detto dominio della funzione; il sottoinsieme di B formato dalle immagini degli elementi di A è detto codominio. Indichiamo il codominio con la lettera C.
Vale la relazione .
Per indicare una funzione si utilizza anche la scrittura:
$$y=f(x)$$
INDICE
