DEFINZIONE
Il dominio naturale della funzione è l’insieme più ampio dei valori che si possono assegnare alla variabile indipendente x affinché esista il corrispondente valore reale y.
Normalmente il dominio naturale non viene assegnato esplicitamente, perché può essere ricavato dall’espressione analitica della funzione.
ESEMPIO
Ad esempio, consideriamo la funzione:
Se sostituiamo a x un valore minore di 2, la radice perde significato.
Il dominio naturale di tale funzione è l’intervallo , con
. In forma abbreviata scriviamo:
D: .
Quando viene assegnata una funzione senza indicare esplicitamente il dominio, si sottintende che esso sia il dominio naturale,
Funzioni uguali
Due funzioni f e g sono uguali se hanno lo stesso dominio D e f(x)=g(x) per ogni x appartenente a D.
ESEMPI
Consideriamo le seguenti funzioni e determiniamo i rispettivi Domini.
e
sono uguali in
, dominio naturale di entrambe.
e
, considerate nel loro dominio naturale, non sono uguali perché non hanno lo stesso dominio.
CLASSIFICAZIONE DELLE FUNZIONI
Funzioni Algebriche
- Funzione Razionale Intera
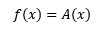
- Funzione Razionale Fratta
Una funzione si dice razionale fratta quando il termine x compare la denominatore
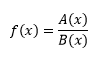
- Funzione Irrazionale
Una funzione è irrazionale quando il termine x compare sotto una radice:
Funzioni Trascendenti
- Funzioni Logaritmiche
Una funzione è logaritmica quando il termine x compare come argomento di un logaritmo:

- Funzioni Esponenziali
Una funzione è esponenziale quando il termine x compare come argomento di un esponenziale:
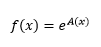
- Funzioni Goniometriche
Una funzione è goniometrica quando il termine x compare come argomento di una funzione goniometrica:
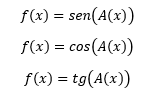
Funzioni composte
Tutte le funzioni sopraelencate si possono classificare come funzioni elementari. Chiaramente potremmo incontrare delle funzioni che sono derivate dalla composizione di queste funzioni elementari.
ESEMPI:
Funzione irrazionale fratta

Funzione logaritmica e irrazionale

Funzione logaritmica e fratta

Di seguito uno schema riassuntivo con il dominio delle funzioni.