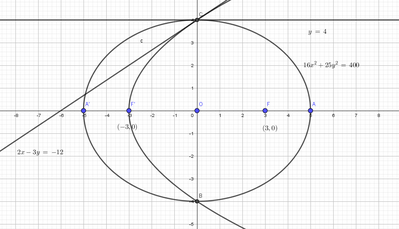
Considera l'ellisse che ha un vertice in $A(5,0)$ e un fuoco in $F(3,0)$. Determina:
a. l'equazione dell'ellisse;
b. il rapporto tra l'area del quadrato inscritto nell'ellisse (avente i lati paralleli agli assi cartesiani) e l'area della regione di piano racchiusa dell'ellisse stessa;
c. l'equazione della parabola, con asse orizzontale, che ha vertice nel fuoco dell'ellisse di ascissa negativa e passa per i punti d'intersezione dell'ellisse con l'asse $y$;
d. le equazioni delle rette tangenti all'ellisse e alla parabola nel loro punto d'intersezione con il semiasse delle ordinate positive;
e. le aree delle due parti in cui la parabola divide la regione di piano racchiusa dall'ellisse.
a. $\frac{x^2}{25}+\frac{y^2}{16}=1 ;$ b. $\frac{80}{41 \pi} ;$ c. $x=\frac{3}{16} y^2-3 ;$ d. $y=4, y=\frac{2}{3} x+4 ;$ e. $10 \pi-16,10 \pi+16$