qualcuno riesci a risolvere e a spiegarmi il seguente problema di trigonometria?
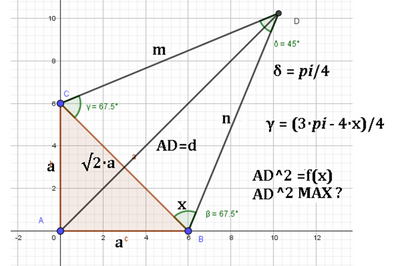
Nel triangolo rettangolo $A B C$ è $\overline{A B}=\overline{A C}=a$. Costruisci, nel semipiano non contenente $A$ e avente come origine la retta $B C$, il triangolo $B D C$, tale che $B \widehat{D C}=\frac{\pi}{4}$ e $B \widehat{C} D=x$. Per quali valori di $x$ è massimo il quadrato della distanza di $A$ da $D$ ?
$$
\left[\overline{A D}^2=\left[3+2 \sqrt{2} \sin \left(2 x-\frac{\pi}{4}\right)\right] a^2, \text { con } 0 \leq x \leq \frac{3 \pi}{4} ; \text { massimo per } x=\frac{3 \pi}{8}\right]
$$