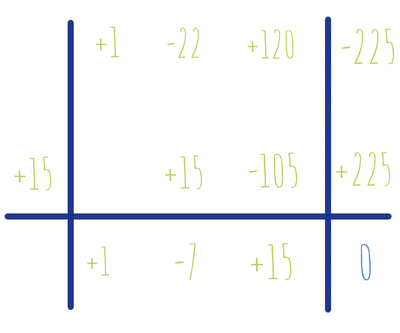
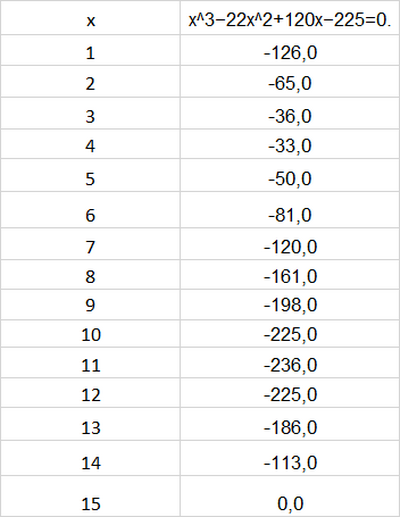
Buondì popolo dei numeri, cercando di risolvere un'equazione mi son ritrovato a questo punto:
$x^3-22x^2+120x-225=0$.
Non vedendo possibili scomposizioni ed essendo in preda di dubbi sulla scomponibilità di questo polinomio, ho deciso di optare per Ruffini! Mi è calato un po' l'entusiasmo poiché i divisori di $225$ sono molteplici, e provarli uno ad uno, provoca una lievissima sofferenza dentro me. 😆
$Divisori\:\left\{\pm 1,\:\pm 3,\pm 5,\pm 15,\:\pm 25,\:\pm 45,\pm 75,\:\pm 225\right\}$
Da qui mi è sorta una curiosità, non esiste un metodo per individuare subito il numero che sto cercando?! Devo davvero provare uno ad uno pregando alla fine esca lo 0? 😆
D'altronde ci vuole anche un po' di tempo, non penso che i matematici non abbiano pensato a un modo per aggirare questo problema! 😏
Il polinomio che ho scritto era per darvi un esempio, in realtà mi son sempre chiesto questa cosa, ogni volta che ho dovuto utilizzare Ruffini e cercare il numero desiderato.
Grazie a chi risponderà 🖐️