[Risolto] Esercizio iperbole

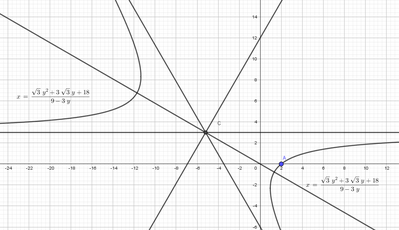
Determino il centro C dell'iperbole:

{y = 3 asintoto orizzontale

{x + √3·y = 0 asse di simmetria

quindi: [x = - 3·√3 ∧ y = 3]----> C( - 3·√3, 3)

L'altro asintoto (obliquo) gode di simmetria assiale rispetto all'asse di simmetria dell'asintoto orizzontale y=3

{η = ((1 - m^2)·x + 2·m·y - 2·m·q)/(1 + m^2)

{μ = (2·m·x + (m^2 - 1)·y + 2·q)/(1 + m^2)

Dove [η,μ] sono le coordinate correnti dell'asintoto stesso.

L'asse di simmetria ha equazione:

y = - √3·x/3 quindi: m = - √3/3 e q =0

{η = ((1 - (- √3/3)^2)·x + 2·(- √3/3)·y - 2·(- √3/3)·0)/(1 + (- √3/3)^2)

{μ = (2·(- √3/3)·x + ((- √3/3)^2 - 1)·y + 2·0)/(1 + (- √3/3)^2)

quindi: 

{η = (x - √3·y)/2

{μ = - (√3·x + y)/2

L'asintoto orizzontale è rappresentato dal punto: [t, 3]

Quindi otteniamo le equazioni parametriche dell'asintoto obliquo dell'iperbole:

{η = (t - √3·3)/2

{μ = - (√3·t + 3)/2

ossia: 

{x = t/2 - 3·√3/2    (cioè: x = η)

{y= - √3·t/2 - 3/2   (cioè: y = μ)

Dalla prima t = 2·x + 3·√3

per sostituzione:

y = - √3·(2·x + 3·√3)/2 - 3/2----> y = - √3·x - 6 asintoto obliquo iperbole)

Determino ora equazione iperbole

E' del tipo:

x = (a·y^2 + b·y + c)/(y - 3)

ossia:

x = (9·a + 3·b + c)/(y - 3) + (a·y + 3·a + b)

Nella seconda parentesi è rappresentato asintoto obliquo

Risolviamo quindi in x quanto trovato sopra:

x = - √3·y/3 - 2·√3

Quindi scriviamo il sistema:

{a = - √3/3

{3·a + b = - 2·√3

{2 = (a·0^2 + b·0 + c)/(0 - 3) (passaggio per A)

Risolvendo si ottiene: [a = - √3/3 ∧ b = - √3 ∧ c = -6]

Quindi:

x = ((- √3/3)·y^2 + (- √3)·y + -6)/(y - 3)

svolgendo i conti:

x = (√3·y^2 + 3·√3·y + 18)/(9 - 3·y)

 

C è il nome del centro, che è un punto; l'iperbole è una curva e si chiama Γ.
* (r ≡ x + (√3)*y = 0) & (s ≡ y − 3 = 0) ≡ (y = - x/√3) & (y = 3) ≡ C(- 3*√3, 3)
-----------------------------
Traslare
* (x = X - 3*√3) & (y = Y + 3)
* r ≡ y = - x/√3 → r' ≡ Y + 3 = - (X - 3*√3)/√3 ≡ Y = - X/√3
* s ≡ y = 3 → s' ≡ Y + 3 = 3 ≡ Y = 0
* A'(2 + 3*√3, - 3)
«... si consideri l'iperbole Γ' passante per il punto A'(2 + 3*√3, - 3), con un asse di simmetria sulla retta "r' ≡ Y = - X/√3" e un asintoto sull'asse X "s' ≡ Y = 0".»
-----------------------------
Ruotare di θ = arctg(- 1/√3) = - π/6 = - 30°
NOTA: dovrei scrivere (ξ, η) ma, per evitare troppi Copia/Incolla, uso (x, y); sia chiaro che non si tratta del riferimento originario.
* (X = x*cos(- π/6) - y*sin(- π/6)) & (Y = x*sin(- π/6) + y*cos(- π/6)) ≡
≡ (X = ((√3)*x + y)/2) & (Y = ((√3)*y - x)/2)
* r' ≡ Y = - X/√3 → r'' ≡ ((√3)*y - x)/2 = - ((√3)*x + y)/2/√3 ≡ y = 0
* s' ≡ Y = 0 → s'' ≡ ((√3)*y - x)/2 = 0 ≡ y = x/√3
* A''(6 + √3, 1)
«... si consideri l'iperbole Γ'' passante per il punto A''(6 + √3, 1), con un asse di simmetria sull'asse x "r'' ≡ y = 0" e un asintoto sulla retta "s'' ≡ y = x/√3". Determinare l'equazione dell'altro asintoto e l'equazione cartesiana di Γ''.»
L'altro asintoto è
* t'' ≡ y = - x/√3
L'equazione cartesiana di ogni iperbole riferita ai suoi assi ha la forma
* (x/a)^2 - (y/b)^2 = ± 1
dove
* i valori (a, b), positivi, sono le lunghezze dei semiassi
* il doppio segno dipende da quale sia l'asse focale
---------------
Il punto A'' è compreso nell'angolo Est dei quattro formati dagli asintoti, quindi i fuochi sono sull'asse x e la forma dell'equazione è
* (x/a)^2 - (y/b)^2 = 1
---------------
La pendenza del primo asintoto è b/a = 1/√3 ≡ b = a/√3, da cui
* (x/a)^2 - (y/(a/√3))^2 = 1
---------------
Il passaggio per A'' impone il vincolo
* (((6 + √3)/a)^2 - (1/(a/√3))^2 = 1) & (a > 0)
da cui
* a = 2*√(3*(3 + √3))
* b = 2*√(3*(3 + √3))/√3 = 2*√(3 + √3)
* Γ'' ≡ (x/(2*√(3*(3 + √3))))^2 - (y/(2*√(3 + √3)))^2 = 1
==============================
RITORNO a t, Γ da
* t'' ≡ y = - x/√3
* Γ'' ≡ (x/(2*√(3*(3 + √3))))^2 - (y/(2*√(3 + √3)))^2 = 1
-----------------------------
Ruotare di - θ = π/6 = 30°
* (x = X*cos(π/6) - Y*sin(π/6)) & (y = X*sin(π/6) + Y*cos(π/6)) ≡
≡ (x = ((√3)*X - Y)/2) & (y = (X + (√3)*Y)/2)
* t'' ≡ y = - x/√3 → (X + (√3)*Y)/2 = - (((√3)*X - Y)/2)/√3 ≡ t' ≡ Y = - (√3)*X
* Γ'' ≡ (x/(2*√(3*(3 + √3))))^2 - (y/(2*√(3 + √3)))^2 = 1 →
→ ((((√3)*X - Y)/2)/(2*√(3*(3 + √3))))^2 - (((X + (√3)*Y)/2)/(2*√(3 + √3)))^2 = 1 ≡
≡ Γ' ≡ - X*Y/(1 + √3) - Y^2/(3 + √3) = 6
-----------------------------
Traslare
* (X = x + 3*√3) & (Y = y - 3)
* t' ≡ Y = - (√3)*X → y - 3 = - (√3)*(x + 3*√3) ≡ t ≡ y = - (√3)*x - 6
* Γ' ≡ - X*Y/(1 + √3) - Y^2/(3 + √3) = 6 → - (x + 3*√3)*(y - 3)/(1 + √3) - (y - 3)^2/(3 + √3) = 6 ≡
≡ Γ ≡ (3 + √3)*x*y + (1 + √3)*y^2 - 3*(3 + √3)*x + 3*(1 + √3)*y + 6*(3 + √3) = 0
-----------------------------
S.E.&O.

Una discussione dettagliata sarebbe lunga. Ometto quindi i calcoli e scrivo solo il procedimento.

Inoltre per me, che non conosco questi argomenti "a colpo sicuro" é richiesto uno sforzo mentale.

L'altro asintoto é la simmetrica di y = 3 rispetto all'asse y = -1/rad(3) * x.

Per determinarla come luogo di punti simmetrici

1) poni P = (t,3)

2) determini il risultato della simmetria assiale secondo le tradizionali formule

x' = ((1-m^2) - 2my - 2mq)/(1 + m^2)

y' = (2mx + (m^2 - 1)y +2q)/(1 + m^2)

 

con q = 0, x = t, y = 3, m = -1/rad(3)

3) elimini t fra le due equazioni trovate e trovi l'altro asintoto

x rad(3) + y + 6 = 0

Per arrivare all'equazione dell'iperbole scrivo

y ( x rad(3) + y) + ax + by + c = 0

Imposto il passaggio per A

 

2a + 0 + c = 0 => c = -2a

y (x rad(3) + y) + ax + by - 2a = 0

Infine si impone attraverso sostituzione e principio di identità dei polinomi

che il punto di incontro degli asintoti (-3 rad(3), 3) sia centro di simmetria

ovvero che l'equazione

(6 - y) [( - 6 rad(3) - x) * rad(3) + 6 - y ] + a(- 6 rad(3) - x ) + b(6 - y) - 2a = 0

sia identica all'originale.

Ne risulta a = - 3 rad(3) e b = 3

per cui

xy rad(3) + y^2 - 3 x rad(3) + 3y + 6 rad(3) = 0

é l'equazione cartesiana richiesta, ed é confermata dal grafico seguente

 

https://www.desmos.com/calculator/ljgqhumewr