Tratteremo di seguito alcune funzioni goniometriche che alla misura dell’ampiezza di ogni angolo associano un numero reale.
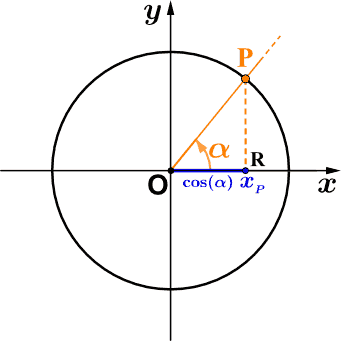
Consideriamo la circonferenza goniometrica e un angolo orientato $\alpha$, e sia P il punto della circonferenza associato ad $\alpha $.
Definiamo coseno e seno dell’angolo $\alpha $, e indichiamo con $\cos \alpha$ e $\sin \alpha $ , l funzioni che ad $\alpha$ associano, rispettivamente, il valore dell’ascissa e quello dell’ordinata del punto :
$$\cos \alpha = x_{B} $$
$$\sin \alpha = y_{B} $$
allora $P( cos \alpha ; \sin \alpha )$
Seno e coseno di un angolo $\alpha$ sono funzioni che hanno come dominio R, perchè per ogni valore di $\alpha$ contenuto in R esiste uno e un solo punto sulla circonferenza.
Avendo rappresentato il seno ed il coseno su circonferenze goniometriche di raggio unitario, qualunque sia la posizione di P sulla circonferenza, la sua ordinata e la sua ascissa assumono sempre valori compresi fra -1 e +1.
I GRAFICI DELLE FUNZIONI SENO E COSENO
E’ possibile costruire il grafico della funzione $y= \sin \alpha $ in $\left[0;2\Pi \right]$ riportando sull’asse x i valori degli angoli e, in corrispondenza, sull’asse y le ordinate dei punti che stanno sulla circonferenza goniometrica.

Analogamente, per ottenere il grafico della funzione coseno, riportiamo sulle ordinate di un piano cartesiano le ascisse dei punti della circonferenza goniometrica in corrispondenza degli angoli.

IL PERIODO
Dopo aver percorso un giro completo, il punto P può ripetere lo stesso movimento quante volte si vuole.
Le funzioni seno e coseno sono quindi periodiche di periodo $2\Pi$. Possiamo scrivere, in modo sintetico:
$$\sin (\alpha +2k\Pi )=\sin \alpha $$
$$\cos (\alpha +2k\Pi )=\cos \alpha $$
con k intero.
Il grafico completo della funzione seno si chiama sinusoide, mentre quello della funzione coseno si chiama cosinusoide. I grafici delle due funzioni sono sovrapponibili con una traslazione di vettore parallelo all’asse x e di modulo $\frac{\Pi }{2}$.
La prima relazione fondamentale
Poichè $P( cos \alpha ; \sin \alpha )$ appartiene alla circonferenza goniometrica, le sue coordinate soddisfano l’equazione $x^2+y^2=1$.
$$\cos ^2\alpha +\sin ^2\alpha =1$$
questa rappresenta la prima relazione fondamentale della goniometria.
Da questa relazione è possibile ricavare $ \sin \alpha $ conoscendo $ \cos \alpha $ e viceversa.
Infatti, se è noto $ \cos \alpha$, si ha: $\sin \alpha =\pm \sqrt{1-\cos ^2\alpha } $
Viceversa, se si conosce $ \sin \alpha $, si ha: $\cos \alpha =\pm \sqrt{1-\sin ^2\alpha } $
INDICE