Consideriamo un angolo orientato $\alpha $ e chiamiamo B l’intersezione fra il lato termine e la circonferenza goniometrica. Definiamo cotangente di $\alpha $ la funzione che associa ad $\alpha $ il rapporto, quando esiste, fra l’ascissa e l’ordinata del punto B:
$$\cot \alpha =\frac{x_B}{y_B} $$
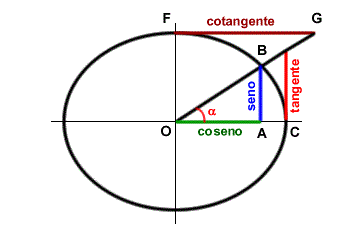
La cotangente di un angolo non esiste quando il numero B si trova sull’asse x, ossia quando l’angolo misura 0, $\Pi $ e tutti i multipli interi di $\Pi $.
Il dominio della funzione cotangente è quindi:
$\alpha\neq k\Pi $ con $k\in Z$
Poiché $\tan \alpha =\frac{y_B}{x_B} $ e $\cot \alpha =\frac{x_B}{y_B} $, risulta $\tan \cdot \alpha \cot \alpha =1$, da cui:
$$\cot \alpha =\frac{1}{\tan \alpha } $$
con $\alpha\neq k\frac{\Pi }{2} $
La condizione posta deriva dal fatto che consideriamo $\frac{1}{\tan \alpha } $, quindi occorre scartare gli angoli in cui non esiste $ \tan \alpha $, cioè $ \alpha= \frac{\Pi }{2}+k \Pi $, e quelli in cui $ \tan \alpha =0$, cioè $ \alpha= 0+k \Pi $ , perciò: $ \alpha \neq k\frac{\Pi }{2}$ .
Dalla definizione di cotangente deriva anche che:
$$\cot \alpha =\frac{\cos \alpha }{\sin \alpha } $$
con $\alpha \neq k\pi$.
Un altro modo di definire la cotangente è attraverso la circonferenza goniometrica.
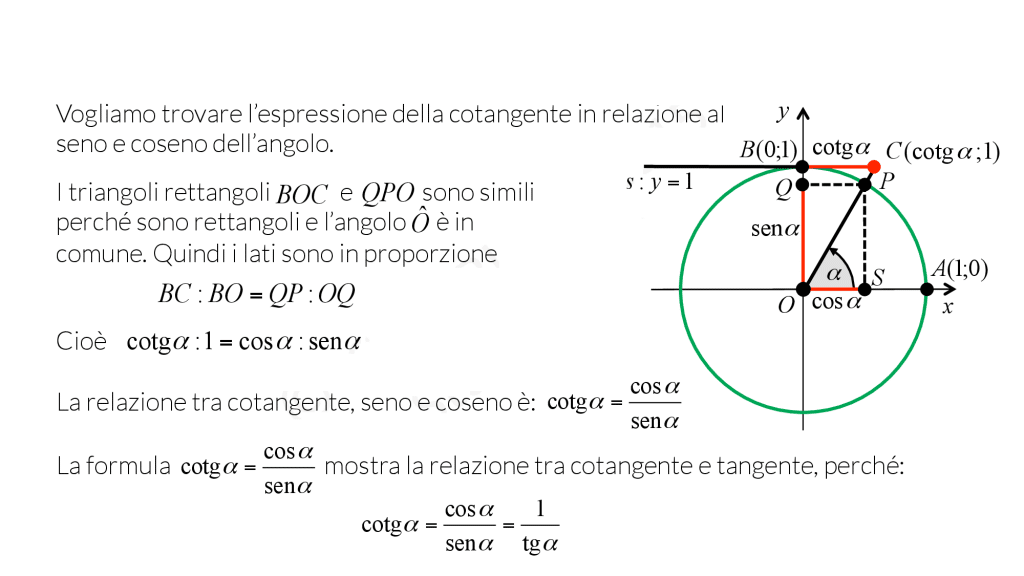
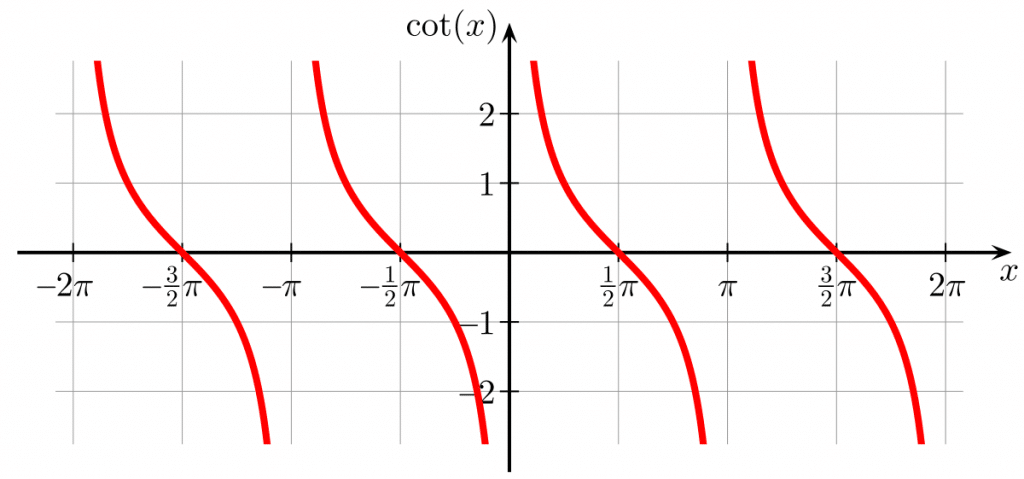
Il grafico della funzione cotangente
Come la tangente, anche la funzione cotangente può assumere qualunque valore reale.
Il periodo della funzione cotangente
In analogia con la tangente, la funzione cotangente risulta periodica di periodo $ \Pi $:
$$\cot (\alpha+k\Pi )=\coth \alpha $$
con $k\epsilon Z$.
INDICE
