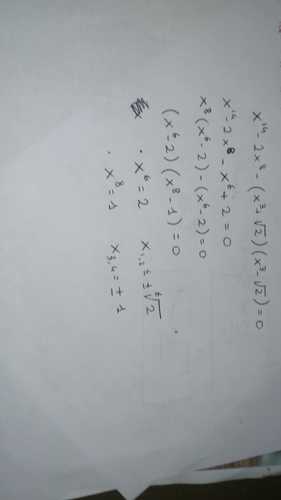Ciao a tutti, mi son imbattuto in questa equazione: $x^{14}-2x^8-\left(x^3+\sqrt{2}\right)\left(x^3-\sqrt{2}\right)=0$.
Sfruttando somma per differenza si avrà: $x^{14}-2x^8-x^6+2=0$. Da qui non riesco più a procedere e non ho idea di come scomporla! 😲
E' possibile utilizzare Ruffini con radice razionale $1$ ma verrebbero una sfilza di termini tutti di grado diverso e mi sembra molto improbabile come metodo di risoluzione.
Le soluzioni dell'equazione sono $x_{1,2}=\:\pm \sqrt[6]{2},\\pm 1$.
E' anche una delle prime equazioni quindi dovrebbe essere semplice eppure non riesco a vedere niente. 😓