[Risolto] problemi sulla corda

Esendo il triangolo ABC inscritto in una semicirconferenza di diametro AB è rettangolo in C.

BC = 2R* sin(CAB) = (8/5)*R

Il triangolo COB è un triangolo isoscele (lato = R) sulla base BC. Determino l'altezza relativa alla base utilizzando il teorema di Pitagora. 

H=radice [L² - (BC/2)²] = (3/5)*R

L'area del triangolo è:

A= (1/2)*BC*H = (12/25)*R²

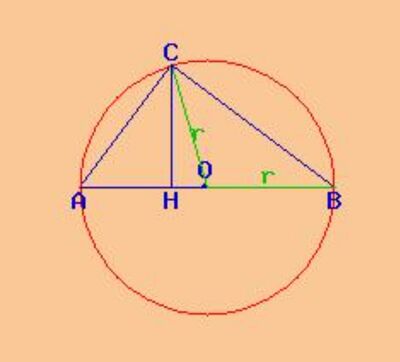
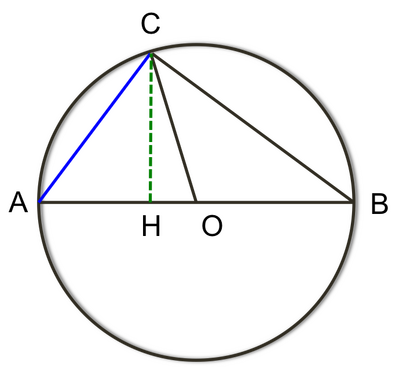
In una circonferenza di diametro AB=2r e centro O, considera una corda AC tale che sinCAB=4/5. Determina l’area del triangolo COB.

(Suggerimento: ricorda le relazioni tra angoli al centro e angoli alla circonferenza e utilizza la formula di duplicazione)

angolo in C = 90°

angolo in A = arcsen 4/5 = 53,13°

angolo in B = 36,87°

AC = 2r*0,6

BC = 2r*0,8

BH = BC^2/2r = √2,56r^2/2r = 1,28 r

CH = r√1,6^2-1,28^2 = 0,960r 

area COB = r*0,96r/2 = 0,48r^2