Problema integrali definiti

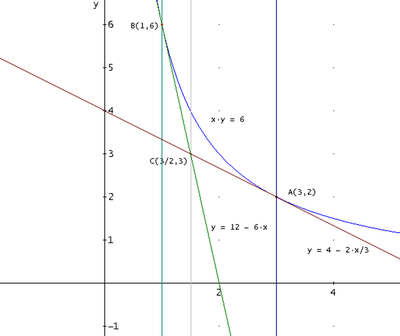
Il punto A ha ascissa 3, quindi ordinata 6/3 =2

A (3,2)

La generica retta per A ha equazione

y -2 = m(x-3)

ovvero y = mx +(2-3m)

Sostituiamo y nell'equazione dell'iperbole:

x*[mx +(2-3m)] =6

ovvero

mx² +(2-3m)x - 6 = 0

Affinché ci sia tangenza deve essere nullo il determinante della precedente equazione. Ovvero

(2-3m)² + 24m =0

ovvero

9 m²+12m+4 = 0

che ha come soluzione

m = - 2/3

quindi la retta tangente ne punto A ha equazione:

ovvero y = -2/3 x +4

 

Il punto B ha ascissa 1, quindi ordinata 6/1 =6

B (1,6)

La generica retta per B ha equazione

y -6 = m(x-1)

ovvero y = mx +(6-m)

Sostituiamo y nell'equazione dell'iperbole:

x*[mx +(6-m)] =6

ovvero

mx² +(6-m)x - 6 = 0

Affinché ci sia tangenza deve essere nullo il determinante della precedente equazione. Ovvero

(6-m)² + 24m =0

ovvero

9 m²+12m+36 = 0

che ha come soluzione

m = -6

quindi la retta tangente ne punto A ha equazione:

ovvero y = -6x +12

 

Il punto C si trova risolvendo il sistema tra le due rette :

y = -2/3 x +4

y = -6x +12

che fornisce

C (3/2, 3)

 

L'area del triangolo mistilineo è data da:

[Integrale definito dell'iperbole da x=1 a x=3] - area dei due trapezi rettangoli delimitati dall'asse delle ascisse e dai lati BC e CB

 

L'integrale indefinito è:

∫6/x dx = 6log(x) + cost.

L'integrale definito per x da 1 a 3 è

6 log(3)-6log(1) = 6.592

 

L'area del primo trapezio è:

A1 = (6+3)*(3/2-1)/2 = 9/4 = 2.25

 

L'area del secondo trapezio è:

A2 = (3+2)*(3-3/2)/2 = 15/4 = 3.75

 

L'area del triangolo mistilineo è:

At = 6.592 - 2.25 - 3.75 = 0.592

@leo

Ciao

xy=6:  x=3------>3y=6------>A(3,2)

xy=6:  x=1------>y=6------->B(1,6)

Determino le rette tangenti nei due punti tramite le formule di sdoppiamento.

Retta tangente in B(1,6):

(6·x + 1·y)/2 = 6 -----> y = 12 - 6·x

Retta tangente in A(3,2)

(2·x + 3·y)/2 = 6----->y = 4 - 2·x/3

Dal sistema delle due equazioni determino C:  x = 3/2 ∧ y = 3

Integro fra 1 e 3/2 la differenza delle funzioni:

y=6/x

y=12-x

6/x - (12 - x) = x + 6/x - 12

L'integrale indefinito è:

6·LN(x) + x^2/2 - 12·x+C tenendo conto che l'iperbole è sopra l'altra

Analogamente integro fra 3/2 e 3 la differenza delle funzioni:

y=6/x

y=4-2/3x

6/x - (4 - 2/3·x) = 2·x/3 + 6/x - 4

Adesso fai tu i calcoli che io sono stanco! Ciao.

 

 

 

TE LO SVOLGO L'ESERCIZIO, MA PRIMA DEVO SPIEGARTI UN PO' DI COSE.
==============================
Caro Leo, avendo ormai "5+ post" dovresti aver già capito che il più probabile significato di "Qualcuno potrebbe aiutarmi?" è semplicemente "Ci sarà un fessacchiotto che mi svolge l'esercizio pronto da copiare, no?".
Se il significato inteso dovesse essere un altro, allora hai fatto malissimo a non esprimerlo chiaramente invece che con tre parole il cui complesso, se preso alla lettera, è stupido e irritante.
L'uso del condizionale (e, per giunta, del verbo potere!) configura la frase come un sondaggio e non come una richiesta (cioè una domanda per sapere, non per ottenere): le risposte possibili vanno da un semplice "Sì!" a "Io potrei, se mi pagassi una birra." fino a "Certo caro, dammi la manina che t'aiuto ad attraversare.".
E le risposte sarebbero le stesse sia con l'indicativo di potere ("Qualcuno può aiutarmi?") che col condizionale di aiutare ("Qualcuno mi aiuterebbe?").
Questo per il lato stupido; il lato irritante è la piaggeria rivelata da "qualcuno".
Se scrivi a un sito dedicato agli alunni in difficoltà ti pare che non ci trovi non solo qualcuno, ma molti che ti possano dare l'aiuto che chiedi?
GIA', QUI STA IL GUAIO: TU NON LO CHIEDI, TI LIMITI A NOMINARLO!
------------------------------
Se avessi letto e ben compreso il
https://www.sosmatematica.it/regolamento/
del sito avresti saputo che esso non è inteso come macchinetta per esercizi, ma come luogo di discussione e consiglio. Perciò avresti dovuto pubblicare anche che cosa hai fatto tentando di svolgerlo e quale difficoltà te l'ha impedito.
Lèggilo bene, prima della prossima domanda!
Se conti di pubblicare qui altre domande (e se vorrai avere risposte ùtili) sarà bene che le presenti dopo aver letto domande, risposte e commenti ai seguenti link
https://www.sosmatematica.it/forum/postid/13048/
https://www.sosmatematica.it/forum/postid/14132/
https://www.sosmatematica.it/forum/postid/14194/
https://www.sosmatematica.it/forum/postid/17873/
https://www.sosmatematica.it/forum/postid/17931/
https://www.sosmatematica.it/forum/postid/19194/
tanto per farti un'idea di come noi responsori più attivi c'immaginiamo che sarebbe bello vedere presentate le richieste.
==============================
ESERCIZIO
Se hai avuto la pazienza di leggere fin qui, ti sei meritato che sia io il fessacchiotto di turno.
------------------------------
L'iperbole
* x*y = 6
è centrata nell'origine con asintoti gli assi coordinati e si svolge nei quadranti dispari con vertici V(± √6, ± √6) coi doppi segni concordi.
---------------
Dalla forma
* y = 6/x
si ricavano i punti A(3, 2) e B(1, 6) e la pendenza
* m(x) = - 6/x^2
che in A e B vale rispettivamente
* in A: m(3) = - 2/3
* in B: m(1) = - 6
---------------
La retta per A(3, 2) di pendenza - 2/3 è
* tA ≡ y = 2 - (2/3)*(x - 3)
---------------
La retta per B(1, 6) di pendenza - 6 è
* tB ≡ y = 6 - 6*(x - 1)
---------------
L'intersezione delle due tangenti è la soluzione di
* (y = 2 - (2/3)*(x - 3)) & (y = 6 - 6*(x - 1)) ≡ C(3/2, 3)
---------------
Dal grafico al link
http://www.wolframalpha.com/input/?i=%5Bx*y%3D6%2C%282-%282%2F3%29*%28x-3%29-y%29*%286-6*%28x-1%29-y%29%3D0%5Dx%3D0to4%2Cy%3D0to7
si vede che l'area S richiesta è la differenza fra quella del triangolo
* T(ABC) = (1/2)*|3*(6 - 3) - 1*(2 - 3) + (3/2)*(2 - 6)| = 2
e quella del segmento iperbolico che è l'integrale fra uno e tre dell'altra differenza d(x) fra la retta congiungente gli estremi
* AB ≡ y = 8 - 2*x
e l'iperbole
* d(x) = 8 - 2*x - 6/x = 2*(4 - x - 3/x)
Quindi
* S = 2 - 2*∫ [x = 1, 3] (4 - x - 3/x)*dx =
= 2 - 2*(4 - 3*ln(3)) =
= 6*(ln(3) - 1) ~= 0.5916737