Buongiorno ragazzi, non riesco a risolvere il seguente problema:
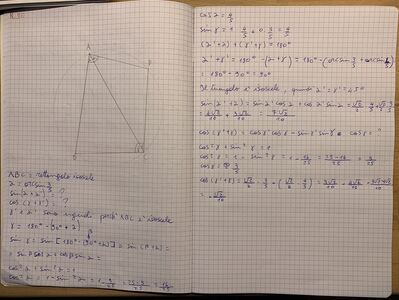
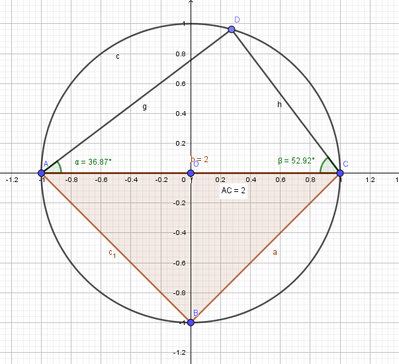
La diagonale AC di un quadrilatero ABCD inscritto in una circonferenza divide il quadrilatero nei due triangoli ABC e ADC. Sapendo che il triangolo ABC è rettangolo isoscele di ipotenusa AC e che DAC = arcsin(3/5), determina sin DAB e cos DCB. Risolvi il problema mediante l'applicazione delle formule di addizione e sottrazione.
Grazie in anticipo
166
punti
Livello 1
Pubblico la mia risoluzione
Ciao di nuovo.
Osservo che AC è diametro della circonferenza circoscritta la quadrilatero e quindi il triangolo ACD è anch'esso rettangolo in D. Con riferimento a quest'ultimo triangolo, chiamo con α e β i relativi angoli acuti.
(vedi figura allegata)
Quindi:
SIN(α) = DC/AC=3/5 ed anche COS(β) = DC/AC = 3/5
La domanda che ora si pone è : determinare:
SIN(α+45)= ? e COS(β+45°)=?
Quindi:
Continuo più tardi devo uscire.
Riprendo
SIN(α + 45°) = SIN(α)·COS(45°) + SIN(45°)·COS(α)
SIN(α + 45°) = √2·COS(α)/2 + √2·SIN(α)/2
Analogamente ottengo:
COS(β + 45°) = √2·COS(β)/2 - √2·SIN(β)/2
Tenendo conto che:
SIN(α) = COS(β) = 3/5
COS(α) = √(1 - (3/5)^2)
COS(α) = 4/5
Analogamente: SIN(β) = 4/5
SIN(α + 45°) = √2·(4/5)/2 + √2·(3/5)/2
SIN(α + pi/4) = 7·√2/10
COS(β + 45°) = √2·(3/5)/2 - √2·(4/5)/2
COS(β + pi/4) = - √2/10
98131
punti
Genius II
Tracciata la figura e constatato che cos a = cos DAC = sqrt (1 - (3/5)^2) = 4/5
per le formule di addizione
sin DAB^ = sin (a + 45°) = sin a cos 45° + cos a sin 45° =
= 3/5 * sqrt(2)/2 + 4/5 * sqrt(2)/2 = 7/10 * sqrt(2);
L'angolo C^ é il supplementare di A^ perché ABCD é inscritto in una circonferenza
DCB^ = 180° - (a + 45°) = 135° - alfa
cos DCB^ = cos (135° - a) = cos 135° cos a + sin 135° sin a =
= - sqrt(2)/2 * 4/5 + sqrt(2)/2 * 3/5 = - sqrt(2)/10
49647
punti
Livello 7
