Tra le parabole di equazione $y=-x^2+2 x+c$, determina la parabola avente il vertice sulla retta $y=2 x+2$. Siano poi $A$ il suo punto di ascissa nulla e $B$ la sua intersezione con il semiasse positivo delle ascisse. Determina un punto $P$ dell'arco $\overparen{A B}$ tale che la differenza tra le distanze di $P$ dagli assi sia massima.
$$
\left[P\left(\frac{1}{2} ; \frac{15}{4}\right)\right]
$$
105
punti
Livello 0
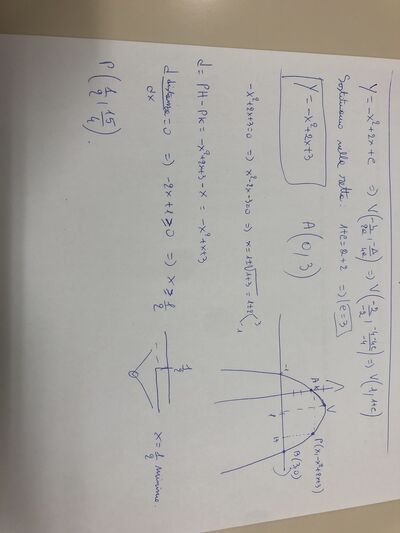
Il vertice della parabola ha coordinate:
$V(\frac{-b}{2a}, \frac{-\Delta}{4a}) = (\frac{-2}{-2}, \frac{-4-4c}{-4}) = (1, 1+c)$
Perché sia sulla retta, poniamo:
$ y = 2x+2$
$ 1+c = 2(1) +2$
$ c = 3$
Dunque la parabola è $ y = -x^2 +2x +3$
Il punto A ha ascissa nulla: A(0,y). Allora l'ordinata è:
$ y = -0^2 +2*0 +3 = 3$
cioè A(0,3).
L'intersezione con il semiasse positivo delle ascisse, di equazione y=0, è:
$ 0 = -x^2 +2x +3$
$ x^2 -2x -3 = 0$
$ x = 3$ o $x=-1$
Dato che consideriamo il semiasse positivo, consideriamo B(3,0).
Il punto P è un punto della parabola, dunque le sue coordinate generiche sono $P(x, -x^2+2x+3)$.
Le distanze dagli assi sono pari al valore delle coordinate: $PK = x$ e $PH = -x^2 +2x +3$.
La differenza delle distanze è dunque:
$d(x) = |PK - PH| = |x-(-x^2 +2x +3)| = |x+x^2 -2x -3| = |x^2 -x -3|$
massimizziamo la distanza calcolandone la derivata:
$d'(x) = \pm (2x-1)$
Questa si annulla per $x=\pm 1/2$, ma dato che stiamo guardando l'arco APB, la x dev'essere positiva, dunque:
$x= +1/2$
da cui
$y = -x^2 +2x +3 = -1/4 +1 +3 = 15/4$
Cioè P(1/2, 15/4)
Noemi
9381
punti
Livello 5
8026
punti
Livello 6
