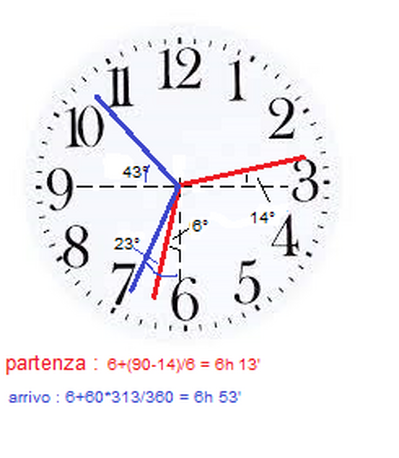
Peter parte dalla città A x minuti dopo le 18:00 e arriva alla città B y minuti dopo le 18:00 dello stesso giorno. Ha notato che sia all’inizio sia alla fine del viaggio la lancetta dei minuti del suo orologio ha formato lo stesso angolo di 110º (gradi) con la lancetta delle ore. Quanti minuti ha impiegato Peter per andare dalla città A alla città B?
A)38
B)39
C)40
D)41
E) nessuna delle precedenti
31
punti
Livello 0
Inizialmente la lancetta dei minuti era 110° indietro rispetto a quella delle ore ( dove prendiamo l'origine )
t é in minuti
@m = - 110° + 6° t
@h = 0° + 30°/60° t = 0.5 t
( la lancetta delle ore percorre uno spicchio di 30° in 1h
e quindi si muove di mezzo grado al minuto )
La risolvente é allora 6 t - 110 - 0.5 t = 110
5.5 t = 110 + 110 => t = 220/5.5 = 40.
36968
punti
Livello 6
6h 53' - 6h 13' = 40'
96644
punti
Genius II
Ciao e benvenuta.
Moto rotatorio uniforme
Il movimento delle lancette è destrorso, la loro posizione è definita a partire da 12.
Quindi alle ore 18.00 la lancetta delle ore è definita dall'angolo 180°, mentre quella dei minuti è definita dall'angolo pari a 0.
Le velocità angolari delle lancette sono:ω e Ω rispettivamente dei minuti e delle ore.
ω = 360/60 = 6------> 6°/minuto
Ω = 360/12 = 30°/h=0.5°/minuto
Le leggi orarie sono:
α = ω·t--------------> α = 6·t
β = 180 + Ω·t------->β = 180 + 0.5·t
Alla partenza si ha:
β - α = 110--------> 180 + 0.5·t - 6·t = 110--------> t = 140/11 minuti
All'arrivo si ha:
α - β = 110-------> 6·t - (180 + 0.5·t) = 110 ------->t = 580/11 minuti
La differenza di t fornisce la soluzione del problema:
(580 - 140)/11 = 40-------> (580 - 140)/11 = 40 minuti
77312
punti
Genius II
