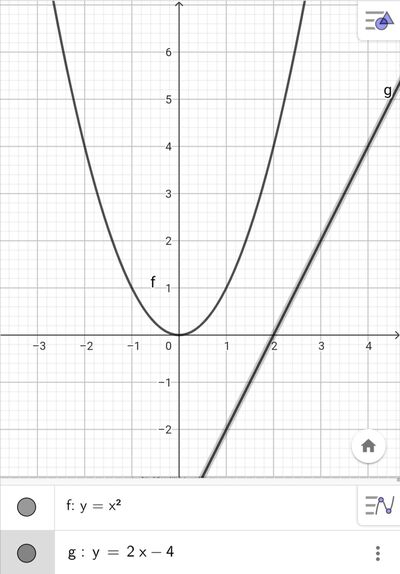
La clausola "per ogni numero naturale n >= 2" è estremamente riduttiva in quanto la disequazione
* u^2 > 2*u - 4 ≡
≡ u^2 - 2*u + 4 > 0 ≡
≡ u^2 - 2*u + 4 >= 3 > 0
è vera quali che siano la natura (naturale, intero, razionale, reale) e il valore di u. Perciò costruire una dimostrazione per induzione si può fare scegliendo un intero qualsiasi come caso base; ad esempio "per ogni intero k >= - 12345" oppure "per ogni intero k >= 0" oppure "per ogni intero k >= 321".
Scegliere "per ogni numero naturale n >= 2" serve solo a semplificare le conclusioni, ma non nel modo dell'esempio (hai ragione a ritenerlo arzigogolato).
---------------
VERIFICA dei casi base (negativo, zero, positivo, particolare).
* (- 12345)^2 > 2*(- 12345) - 4 ≡
≡ 152399025 > 0 > - 24694 < 0 ≡ Vero
* 0^2 > 2*0 - 4 ≡
≡ 0 > - 4 < 0 ≡ Vero
* 321^2 > 2*321 - 4 ≡
≡ 103041 > 638 ≡ Vero
---------------
IPOTESI INDUTTIVA
Si supponga vera la disequazione
* k^2 > 2*k - 4
per un particolare intero k >= valore del caso base.
---------------
TESI DELL'INDUZIONE
* (k + 1)^2 > 2*(k + 1) - 4
---------------
DIMOSTRAZIONE INDUTTIVA (più "semplice", voglio sperare!)
Si sviluppa il quadrato di binomio a primo membro e si sviluppa e riduce il secondo membro.
* (k + 1)^2 > 2*(k + 1) - 4 ≡
≡ k^2 + 2*k + 1 > 2*k + 2 - 4 ≡
≡ k^2 + 2*k + 1 > 2*k - 2
Si sottrae membro a membro il binomio 2*k + 1.
* k^2 + 2*k + 1 > 2*k - 2 ≡
≡ k^2 + 2*k + 1 - (2*k + 1) > 2*k - 2 - (2*k + 1) ≡
≡ k^2 > - 3
Si introduce l'ipotesi induttiva.
* k^2 > 2*k - 4 > - 3 ≡ k > 1/2
E si riconosce l'utilità di scegliere un caso base naturale e non genericamente intero.