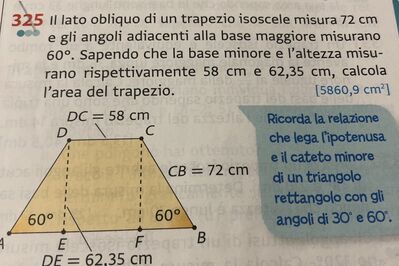
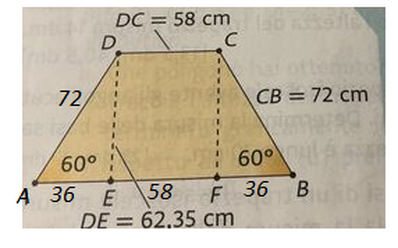
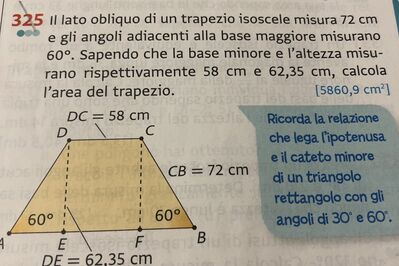
Il lato obliquo di un trapezio isoscele misura $72 cm$ e gli angoli adiacenti alla base maggiore misurano $60^{\circ}$. Sapendo che la base minore e l'altezza misurano rispettivamente $58 cm$ e $62,35 cm$, calcola I'area del trapezio.
$\left[5860,9 cm ^2\right]$