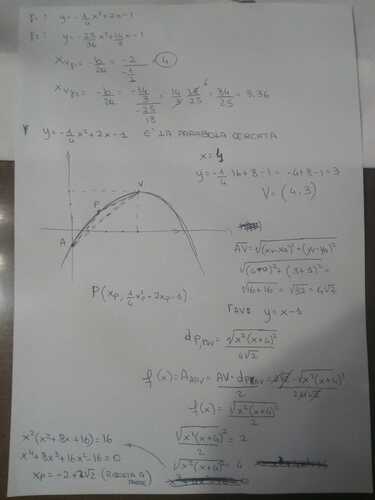
Delle due parabole con asse parallelo all'asse y passanti per A(0 ;-1) e tangenti alle rette y=3x e y=-2x+15, trova quella il cui vertice V ha ascissa maggiore. Sull'arco AV di tale parabola considera un punto P di ascissa x e, indicata con $A (A P V)$ l'area del triangolo $A P V,$ traccia la funzione $f(x)= A (A P V)$ Individua il punto P per cui si ha f(x)=2.
Trova poi l'equazione della circonferenza con centro nel vertice della parabola e passante per il suo fuoco. Spiega perché la circonferenza è tangente alla direttrice.