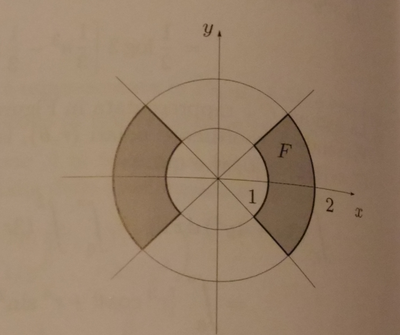
∫∫ arctan(y/x) dx dy dove 1<=x^2 + y^2 <= 4 & |y| <= |x|
Il dominio è nell'immagine caricata.
Uso le coordinate polari : x = rcos(θ)
y = r sen(θ)
det J = r
trovo che la funzione diventa ∫∫ arctan(tan(θ)) r dr dθ
con 1 <= r <= 2 & (0 <= θ <= π/2) U (3π/4 <= θ <= 5π/4) U ( 7π/4 <= θ <= 2π)
Posso fare la semplificazione arctan(tan(θ)) = θ anche per angoli fuori dall'intervallo (-π/2, π/2)?
Se non fosse possibile come devo risolverlo?
Secondo
il libro la soluzione dell'integrale vale 0.
1352
punti
Livello 3
Ciao!
Il fatto che l'integrale faccia zero possiamo capirlo immediatamente perché il dominio è simmetrico rispetto l'origine (in tutte le direzioni) e l'arcotangente è una funzione dispari, quindi verrà sicuramente zero l'integrale.
Per quanto riguarda l'integrazione:
sì, puoi fare $arctan(tan(\theta))= \theta$ solo per $\theta \in (-\frac12 \pi; \frac12 \pi) $, quindi è buona cosa ridurre l'integrale grazie alle sue simmetrie per studiare solamente il caso nell'intervallo che ci interessa.
Notiamo che:
$arctan(tan( - \theta )) = arctan(-tan(\theta)) = - \arctan(tan(\theta)) $
quindi possiamo ridurci a studiare l'integrale per $\theta \in [-\frac14 \pi ; \frac14 pi]$
Proviamo a farlo "a mano":
$\int \int \theta r dr d \theta = \frac14 r^2 \theta^2 $
Ma $ r \in [1,2] $ e $\theta \in [-\frac14 \pi ; \frac14 pi] $
quindi:
$ \frac14 \theta^2 (4-1) = \frac34 \theta^2 = $
$= \frac34 (\pi^2 \frac{1}{16}-\pi^2 \frac{1}{16}) = 0 $
5515
punti
Livello 5
Grazie mille per la risposta!
