[Risolto] aiutooooo

Quindi sono da vedere i punti:

c) Trova il punto Q su in modo che i segmenti AP e BQ siano le basi di un trapezio.

A(0,1) ; P(1/4,3/8) ; B(1,0) Q(?,?)

calcolo coefficiente angolare del segmento AP:

mAP=(3/8 - 1)/(1/4 - 0) = - 5/2

Determino retta per B con questo coefficiente angolare:

y - 0 = - 5/2·(x - 1)------> y = 5/2 - 5·x/2

Metto a sistema:

{y = 5/2 - 5·x/2

{x = - y^2 + 1

Risolvo ed ottengo:

x = 1 ∧ y = 0 ed è B(1,0)

v

x = 21/25 ∧ y = 2/5 ed è Q(21/25,2/5)

d) Calcola l'area del trapezio.

A(0,1) ;

P(1/4,3/8) ;

B(1,0)

Q(21/25,2/5)

A(0,1) 

Area APBQ=

=1/2·ABS(0·3/8 + 1/4·0 + 1·2/5 + 21/25·1+

- (0·2/5 + 21/25·0 + 1·3/8 + 1/4·1)) = 123/400

 

 

Potresti per favore leggere il regolamento del sito ed evitare in futuro "aiutoooo" nel titolo? Grazie.

Dopo le scuse, ti va bene se te lo imposto? poi semmai mi dici dove trovi difficoltà.

metti a sistema le due equazioni e sostituisci $x$ nella prima:

$y=2(-y^2+1)^2-3(-y^2+1)+1$

svolgi e trovi

$2y^4-y^2-y=0$

una radice si vede chiaramente vale $y=0$

ti rimane

$2y^3-y-1=0$

e questa si vede che una radice è $y=1$

ti rimane

$2y^2+2y+1=0$

questa equazione non ha soluzioni nei numeri reali (discriminante negativo), quindi hai soltanto due punti di intersezione:

$A(1,0)$ e $B(0,1)$

adesso sai come andare avanti?

Evidentemente non hai ancora letto il
https://www.sosmatematica.it/regolamento/
del sito. Leggilo, ti sarà utile (specie per "titolo significativo", "evitare", "trascrivere", ...).
Poi ci sono anche alcune tristi verità che il Regolamento, per pudore, ignora.
"aiut..." nel campo "Titolo" ≡ richiedente SCEMO.
Il motivo è presto detto: pubblicare una domanda su un sito di aiuti vuol dire che l'aiuto fa parte della ragione sociale, è SUPERFLUO E IRRITANTE sentirselo chiedere.
Se non lo capisci da te vuol dire che le tue facoltà cognitive necessitano di un po' d'allenamento in più; e allora, se non capisci una cosa così banale, capiresti mai la mia risposta a un problema che banale non è?
Tanto vale che non perda tempo a risponderti.
Adesso però ho tempo e posso rischiare di sprecare una risposta: spero che un po' tu la comprenda, più nella logica che nei valori.
------------------------------
A) Il sistema di grado quattro (due per due) delle parabole (α, β) ha quattro soluzioni: se ne ha esattamente due reali allora quelle sono le coordinate di A e B; se no, lo svolgimento s'interrompe perché il testo si basa su un'ipotesi falsa.
* α ≡ y = 2*x^2 - 3*x + 1 ≡ y = - 1/8 + 2*(x - 3/4)^2
* β ≡ x = - y^2 + 1 ≡ x = 1 - (y - 0)^2
* (x = 1 - y^2) & (y = - 1/8 + 2*(x - 3/4)^2) ≡
≡ (x, y) in {(0, 1), (1, 0), ((2 - i)/2, (- 1 - i)/2), ((2 + i)/2, (- 1 + i)/2)}
quindi
* A(0, 1), B(1, 0)
Vedi
http://www.wolframalpha.com/input?i=%5Bx%3D1-y%5E2%2Cy%3D-1%2F8--2*%28x-3%2F4%29%5E2%5Dx%3D-1to2
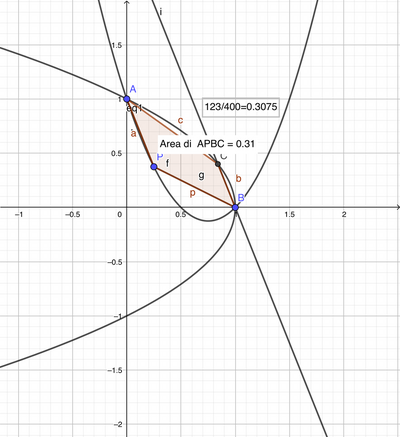
dove l'arco AB di α è quello concavo in alto e l'arco AB di β è quello concavo a sinistra.
------------------------------
B) L'arco AB di α è
* (y = - 1/8 + 2*(x - 3/4)^2) & (0 <= x <= 1)
quindi il cursore P di cui determinare l'opportuna posizione è
* P(p, - 1/8 + 2*(p - 3/4)^2) & (0 <= p <= 1)
e i quadrati delle sue distanze dagli estremi sono
* |PA|^2 = 2*(2*p^2 - 6*p + 5)*p^2
* |PB|^2 = 2*(2*p^2 - 2*p + 1)*(p - 1)^2
da cui
* "BP^2 - AP^2 = 1/4" ≡
≡ (2*(2*p^2 - 2*p + 1)*(p - 1)^2 - 2*(2*p^2 - 6*p + 5)*p^2 - 1/4 = 0) & (0 <= x <= 1) ≡
≡ (p^2 - 2*p + 7/16 = 0) & (0 <= p <= 1) ≡
≡ p = 1/4
e poi
* P(1/4, - 1/8 + 2*(1/4 - 3/4)^2) & (0 <= 1/4 <= 1) ≡
≡ P(1/4, 3/8)
------------------------------
C) Il segmento AP di estremi A(0, 1), P(1/4, 3/8), lungo √29/8, è
* (y = 1 - (5/2)*x) & (0 <= x <= 1/4)
ed è parallelo ad ogni retta del fascio
* r(q) ≡ y = q - (5/2)*x
fra queste quella per B(1, 0)
* r(5/2) ≡ y = (5/2)*(1 - x)
che interseca β in
* (y = (5/2)*(1 - x)) & (x = 1 - y^2) ≡
≡ Q(21/25, 2/5) oppure B(1, 0)
---------------
Il segmento BQ è lungo 2*√29/25
---------------
La distanza fra le due parallele è
* h = 3/√29
------------------------------
D) L'area S del trapezio APBQ è il prodotto dell'altezza per la media delle basi
* S = h*(|AP| + |BQ|)/2 = (3/√29)*(√29/8 + 2*√29/25)/2 = 123/400