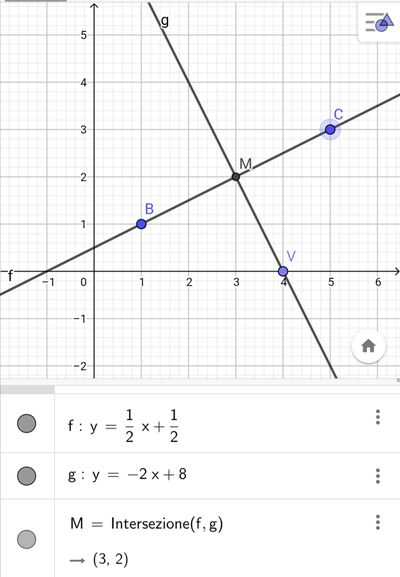
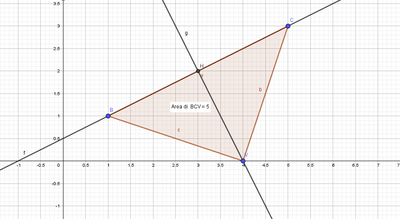
Determina le coordinate dei vertici B e C del triangolo isoscele BCV, di vertice V (4; 0) e di area 5, sapendo che la retta BC ha equazione y = 1/2 x + 1/2
Risposta : B(1; 1), C(5; 3).
Sto provando a risolverlo da tutto il pomeriggio, ma non riesco a trovare il modo. Per cortesia, se qualcuno può aiutarmi, gliene sarò grato. Grazie anticipatamente.
1502
punti
Livello 1
Ciao.
Intanto il disegno:
Il triangolo è isoscele di altezza pari a VH che risulta pure mediana e bisettrice in V.
Conosci l'equazione del lato BC y = 1/2·x + 1/2-----> m = 1/2
Determini l'equazione dell'altezza VH
m=-2 (condizione di perpendicolarità)
quindi
y - 0 = - 2·(x - 4)------> y = 8 - 2·x
Determini le coordinate di H:
{y = 1/2·x + 1/2
{y = 8 - 2·x
Risolvi ed ottieni: [x = 3 ∧ y = 2]-------> H(3,2)
Altezza=VH=√((4 - 3)^2 + (0 - 2)^2) = 2·5/√5 cm = h
Con formula inversa ha la base b:
b=2A/h= 2*5/√5----->b =2·√5
La distanza di B da H = √5
Quindi B(x,x/2+1/2)
√((x - 3)^2 + (x/2 + 1/2 - 2)^2) = √5
risolvi ed ottieni: x = 5 ∨ x = 1
Da cui deduci le soluzioni date!
B(1,1) e C(5,3)
94774
punti
Genius II
Grazie come sempre ; molto chiaro, preciso e facilmente comprensibile. Complimenti
Ciao @beppe
Grazie dei complimenti. Buona serata.
@lucianop 👍👍👍
Il punto H, piede della perpendicolare coincide con il punto medio M del segmento BC essendo il triangolo isoscele sulla base BC
y= - 2x + 8 retta passante per V e perpendicolare alla base del triangolo isoscele
Quindi il punto
B=(1, 1)
C=(5,3)
Ciao Beppe,
Ti ho scritto una possibile soluzione.
Se hai dubbi fammi sapere.
Buona serata
76754
punti
Genius II
Ciao, innanzitutto grazie per la risposta sempre celere ; ci sono 2 punti su cui gentilmente avrei bisogno di chiarimenti : 1) nel primo sistema cosa rappresenta l'equazione y = -2x + 8? 2) Non ho capito come hai calcolato la distanza di V dalla retta contenente il lato BC, cioè non mi è chiaro da dove hai ricavato i dati : 5/2 * 2/rad5 ; 3) Nell'ultima parte quando hai determinato B e C imponendo che PM = rad 5, hai impostato la seguente equazione : (xp -3) ^2 + (1/2xp -3/2)^2 = 5. Come sei giunto a inseriree questi dati : cioè xp -3 ???? e 1/2 xp -3/2???? = 5 ????
In attesa di una tua risposta, auguro a te e famiglia una buona serata e per domani una serena giornata di festa.
Giuseppe
L'equazione y= - 2x +8 rappresenta la retta passante per il vertice V e perpendicolare alla base del triangolo isoscele, quindi la retta contenente l'altezza rispetto alla base. Il punto di intersezione tra questa retta è la retta y= 1/2*x + 1/2 è anche il punto medio M del segmento BC poiché il triangolo è isoscele.
Essendo M il punto medio di BC e avendo calcolato che la base è 2*radice (5) dovrà essere MB=MC= RADICE (5)
Il generico punto P appartenente alla retta contenente la base ha coordinate (xp, 1/2*xp + 1/2). Quindi se impongo che MP=radice (5) determino le coordinate di B, C
Ho utilizzato la formula della distanza tra due punti. Il punto P e il punto M(3,2)
Ti ringrazio per gli auguri che ricambio di cuore. Spero di averti chiarito i dubbi. Eventualmente scrivimi. Buona serata
Sì ora è tutto chiaro; scusami per le domande, ma, se non capisco, chiedo. Devo vederci chiaro...sono fatto così. Ancora vivi ringraziamenti.
