ciao a tutti… potete aiutarmi con lo studio della funzione fratta f(x)=[radiceq(x^2-2)]-x/[radiceq(x^2-3)]
ciao a tutti… potete aiutarmi con lo studio della funzione fratta f(x)=[radiceq(x^2-2)]-x/[radiceq(x^2-3)]
Lo studio di una funzione risiede in diversi passaggi che riporto qui di seguito:
1) Dominio della funzione
2) Intersezione con gli assi cartesiani
3) Studio di parità e disparità
4) Studio del segno di una funzione
5) Limiti agli estremi del dominio
6) Studio della derivata prima: punti di massimi e minimi relativi e/o assoluti
7) Studio della derivata seconda: convessità e punti di flesso
8) Grafico della funzione
Della funzione da te richiesta, cosa vorresti sapere in particolare?
Vorrei sapere il dominio e il grafico della funzione per favore!
y = (√(x^2 - 2) - x)/√(x^2 - 3)
La funzione non è né pari né dispari
1) Dominio della funzione (C.E.)
Devi risolvere il sistema:
{x^2 - 2 ≥ 0
{x^2 - 3 > 0 (è al denominatore!)
Quindi: [x < - √3, x > √3]
2) Intersezione con gli assi cartesiani
Devi risolvere il sistema:
{y = (√(x^2 - 2) - x)/√(x^2 - 3)
{y = 0
Quindi:√(x^2 - 2) - x = 0 che non ammette soluzioni reali con asse x. Nessuna intersezione.
Con asse delle y nessuna in quanto per x=0 la funzione non è definita.
3) Studio di parità e disparità
detto sopra
4) Studio del segno di una funzione
(√(x^2 - 2) - x)/√(x^2 - 3) > 0 se x < - √3
(√(x^2 - 2) - x)/√(x^2 - 3) < 0 se x > √3
5) Limiti agli estremi del dominio (C.E.)
per x--->-inf si ha:
LIM((√(x^2 - 2) - x)/√(x^2 - 3))=2
x--->-inf
per x--->- √3 - si ha: N(x) =1+√3 e al D(x)=0+ quindi y--->+inf
per x--->+ √3 + analogamente y---->-inf
Per gli altri punti se ho tempo e voglia risponderò dopo. Ciao.
Per trovare il dominio di una funzione fratta, bisogna studiare numeratore e denominatore.
Data la funzione
N≥0: , allora,
Risolvendo tali sistemi separatamente otteniamo:
L’intersezione che si ottiene per il primo sistema è la seguente:
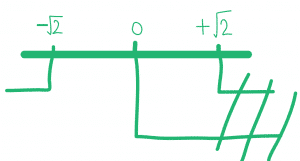
L’intersezione che si ottiene per il secondo sistema è la seguente:
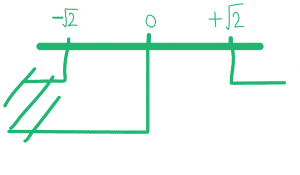
Quindi visto che si tratta di un unione tra sistemi, la soluzione per il numeratore è:
N:
Ora dobbiamo studiare il denominatore:
D>0:
quindi la soluzione per il denominatore è:
D:
Studiamo ora il segno della funzione fratta f(x)>0:
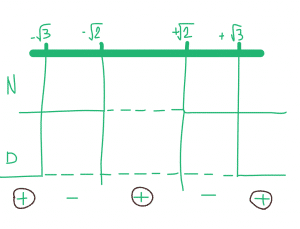
Quindi la soluzione finale è:
Il grafico finale che si ottiene, dopo i vari passaggi dello studio della funzione data, è il seguente:
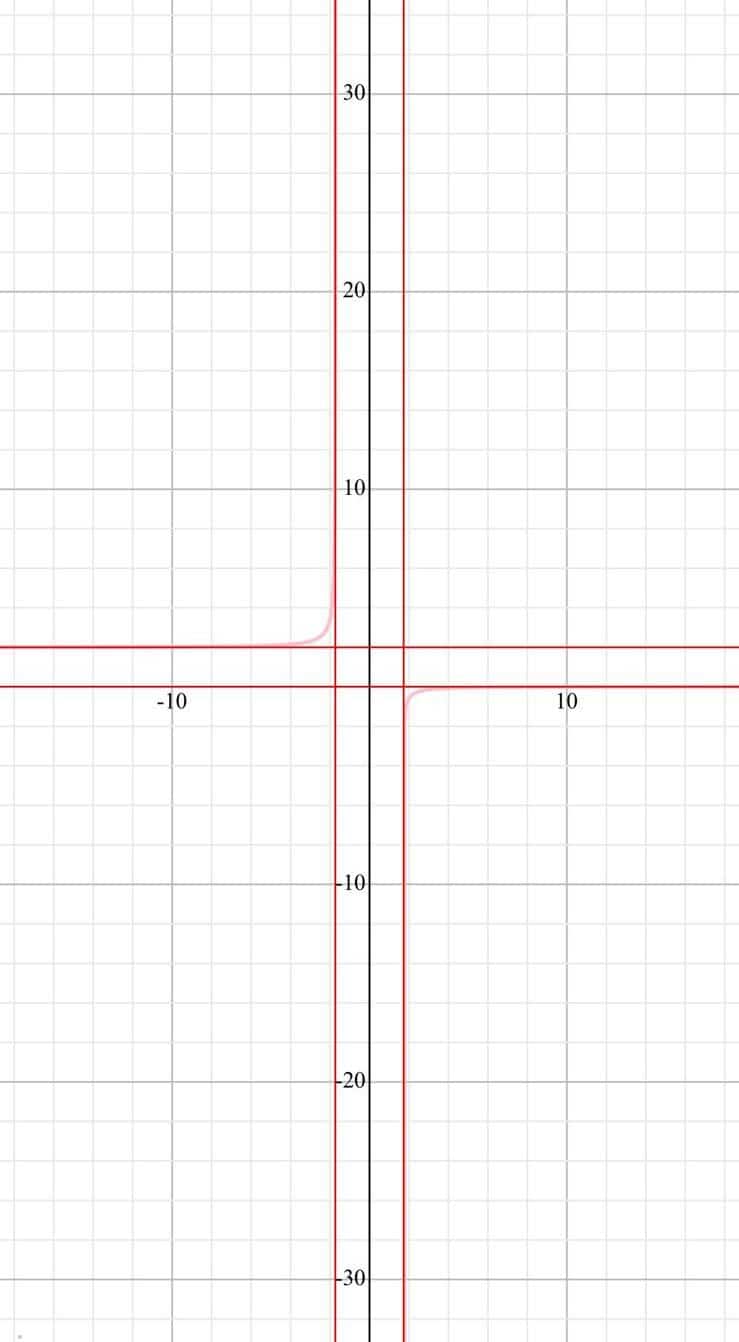
I punti di flesso, se sono presenti, si ricavano studiando la derivata seconda.
Poniamo la funzione maggiore di zero e studiamo il segno del numeratore e del denominatore.
Una volta ottenuti i rispettivi punti x , compiliamo il quadro dei segni della derivata seconda e segniamo gli intervalli in cui il grafico della funzione ha concavità verso l’alto e quelli in cui la concavità è verso il basso.
Nel passaggio dal cambio di segno, ad esempio nel passare dalla concavità positiva alla concavità negativa, troviamo dei punti di flesso che li otteniamo ponendo la x trovata a zero. Se invece abbiamo concavità positiva affiancata da concavità positiva, non abbiamo cambio di segno quindi il punto di flesso non ci sarà. In poche parole, si ottengono flessi solo quando i valori trovati dalla derivata seconda cambiano di segno, posti sulla linea temporale in ordine crescenti.
Per trovare le equazioni delle tangenti inflessionali, sappiamo che il coefficiente angolare della retta (m) si ottiene sostituendo il punto di flesso nella derivata prima