[Risolto] Studio della funzione

Ciao!

$$ y = a^{bx+2}+c$$

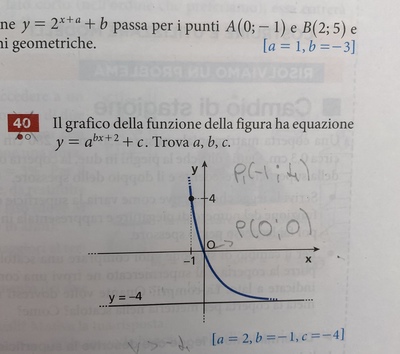
La funzione passa per $P(0;0)$, $P_1(-1; 4)$ e inoltre per $x \rightarrow + \infty$ ha asintoto $y = -4$, quindi:

$\begin{cases} a^{b \cdot 0 +2} +c = 0 \\ a^{b\cdot(-1)+2}+c = 4 \\a^{b \cdot (+\infty) +2} +c = -4 \end{cases} $

$\begin{cases} a^{2} +c = 0 \\ a^{-b+2}+c = 4 \\a^{b \cdot (+\infty) } +c = -4 \end{cases} $

$\begin{cases} c = -a^{2} \\ a^{-b+2}-a^{2}= 4 \\a^{b \cdot (+\infty) } -a^{2} = -4 \end{cases} $

$\begin{cases} c = -a^{2} \\ a^{-b}\cdot a^{2}-a^{2}= 4 \\a^{b \cdot (+\infty) } -a^{2} = -4 \end{cases} $

$\begin{cases} c = -a^{2} \\ a^{-b}\cdot a^{2}-a^{2}= 4 \\a^{b \cdot (+\infty) } -a^{2} = -4 \end{cases} $

Per avere asintoto orizzontale, l'esponenziale deve tenere a zero necessariamente (altrimenti tenderebbe all'infinito, rendendo vani i nostri sforzi di ottenere l'asintoto), quindi

$b < 0 \Rightarrow a^{b \cdot +\infty} = 0 $

quindi l'ultima condizione diventa: $-a^2 = -4 \Rightarrow a = 2 $

Quindi: 

$c = -4 $

e, di conseguenza:

$4\cdot 2^{-b}-4 = 4 $

$ 2^{-b}-1 = 1 $

$2^{-b} = 2 $

$-b = 1 $

$b = -1$

La funzione quindi è: 

$$ y = 2^{-x+2} -4 $$ 

dominio: essendo un esponenziale, $D_f = \mathbb{R} $

intersezioni:

con l'asse $x$: dal grafico sappiamo che è $(0,0)$.

con l'asse $y$: dal grafico sappiamo che è $(0,0)$.

segno; $2^{-x+2} -4> 0$
$2^{-x+2} > 4 \Rightarrow -x +2 > 2 \Rightarrow -x > 0 \Rightarrow x < 0 $

Limiti: $\lim_{x \rightarrow + infty} f(x) = -4 $ Asintoto orizzontale

$\lim_{x \rightarrow - \infty} 2^{-x+2} -4  = 2^{+\infty} = + \infty$

 

Non ha altri asintoti.

Derivata prima:  $2^{-x+2}\cdot(-1)\cdot \log(2) = -\log(2)\cdot2^{-x+2} > 0 $

$\Rightarrow \log(2) \cdot 2^{-x+2} < 0 \Rightarrow \forall x $

La funzione è sempre decrescente.

Non ha minimi o massimi (nel senso di punti stazionari).

Derivata seconda: $-\log(2)2^{-x+2}\cdot(-1)\cdot \log(2)$

$ \log(2)^2 \cdot 2^{-x+2}> 0 \Rightarrow \forall x \Rightarrow$ la concavità della funzione è sempre positiva.

Allora, la funzione deve passare per l'origine, quindi

$0=a^2+c$ questo ci dice che $c=-a^2$, quindi la funzione può essere scritta come

$y=a^{bx+2}-a^2=a^2(a^{bx}-1)$

inoltre 

$\lim_{x \to +\infty} y = -4$

cioè si deve annullare il termine $a^{bx}$, quindi $b$ deve essere negativo.

resta:

$\lim_{x \to +\infty} y=-a^2=-4$ e quindi $a=2$ (a può essere soltanto positivo, essendo una base di un esponenziale)

Quindi 

$y=4(2^{bx}-1)$

adesso imponiamo il passaggio per $P(-1,4)$:

$4=4(2^{-b}-1)$ --> $1=2^{-b}-1$ --> $2=2^{-b}$ 

quindi $-b=1$ e pertanto $b=-1$

La funzione in definitiva è:

$y=4(2^{-x}-1)$

Tale funzione è definita in tutto $R$, dal grafico sai già che interseca gli assi solo nell'origine e ha un asintoto orizzontale per x tendente a +infinito pari a $y=-4$

A questo punto non so se sai fare le derivate, ma in realtà non ce ne è bisogno in quanto la tua funzione è un esponenziale negativo ed è noto che non ha punti di massimo/minimo relativi, la derivata è continua e sempre negativa, quindi la funzione è sempre decrescente. la concavità è sempre verso l'alto e non ha flessi.

la derivata prima ti ricordo si calcola usando la formula:

$f(x)=a^x$ --> $f'(x)=a^x ln(a)$  

senza dimenticare la derivata di funzione composta

Quindi nel nostro caso:

$f'(x)=-4*2^{-x} ln(2)$ 

 

La curva Γ ha equazione della forma
* Γ(a, b, c) ≡ y = a^(b*x + 2) + c
e, nel grafico quotato, mostra le seguenti proprietà geometriche
1) è definita e decrescente ovunque
2) ha l'asintoto y = - 4
3) passa per l'origine
4) passa per (- 1, 4)
dalle quali si possono trarre le informazioni sufficienti a definire l'equazione.
---------------
3) 0 = a^(b*0 + 2) + c ≡ c = - a^2
* Γ(a, b) ≡ y = a^(b*x + 2) - a^2 ≡ y = (a^(b*x) - 1)*a^2
---------------
4) 4 = (a^(b*(- 1)) - 1)*a^2 ≡ b = 2 - log(a, a^2 + 4) = 2 - ln(a^2 + 4)/ln(a)
* Γ(a) ≡ y = (a^((2 - log(a, a^2 + 4))*x) - 1)*a^2 ≡
≡ y = (a^(2*x)/((a^2 + 4)^x) - 1)*a^2
---------------
2) lim_(x → ∞) (a^(2*x)/((a^2 + 4)^x) - 1)*a^2 = - a^2 = - 4 ≡ a = ± 2
quindi ci sono due possibili soluzioni
---------------
2a) a = - 2; b = 2 - ln(8)/(ln(2) + i*π); c = - 4.
* Γ ≡ y = ((- 2)^((ln(8)/(ln(2) + i*π))*x) - 1)*4 ≡
≡ y = 4*(8^x - 1).
---------------
2b) a = + 2; b = 2 - 3 = - 1; c = - 4.
* Γ ≡ y = (2^((2 - log(2, 2^2 + 4))*x) - 1)*2^2 ≡
≡ y = 4*(2^(- x) - 1).
---------------
1a) d/dx 4*(8^x - 1) = ln(8)*2^(3 x + 2) < 0 ≡ FALSO per x reale
---------------
1b) d/dx 4*(2^(- x) - 1) = - ln(2)*2^(2 - x) < 0 ≡ VERO per ogni x reale
---------------
CONCLUSIONE
La funzione sub 2b
* y = 4*(2^(- x) - 1)
è quella che soddisfà a tutt'e quattro i requisiti.

Tutto il richiesto "studio" è nelle proprietà geometriche e al punto 1b.