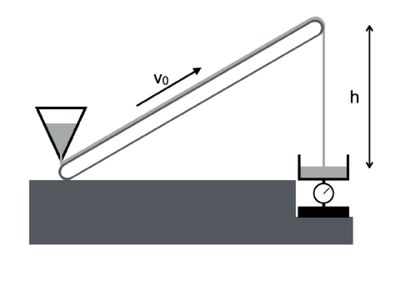
1) In intervallo di tempo $\Delta t$ una quantità di sabbia pari a $\frac{dm}{dt} * \Delta t$ entra sul nastro e una stessa quantità ne esce. La quantità che esce dal nastro ha energia potenziale $\frac{dm}{dt}* \Delta t *g *h$, prendendo il riferimento del potenziale alla quota di ingresso, mentre l'energia potenziale della sabbia che sale sul nastro nello stesso tempo è nulla (altezza nulla dal riferimento).
Analogamente l'energia cinetica della sabbia che esce sarà pari a
$\frac{1}{2} \frac{dm}{dt} \Delta t v_0^2$
mentre quella che entra sarà nulla (si assume che la sabbia non abbia velocità iniziale, dato che viene detto che la sabbia è depositata sul rullo da un altezza trascurabile).
Pertanto la potenza sarà pari alla variazione di energia potenziale fornita alla sabbia, data solo dalla differenza tra quella che esce e quella che entra sul nastro diviso tale tempo $\Delta t$ (la sabbia che sta sul rullo invece è sempre la stessa quindi non varia la sua energia potenziale), a questo si somma la variazione di energia cinetica con le stesse considerazioni, tutto diviso per tempo:
$P=\frac{dm}{dt} g h+\frac{1}{2} \frac{dm}{dt} v_0^2$
2) Occorre prima trovare la velocità $v_f$ con cui la sabbia cadendo giunge sulla bilancia. Questa si può trovare imponendo che la variazione di energia cinetica tra inizio e fine caduta sia pari alla variazione di energia potenziale. Consideriamo sempre una massa di sabbia pari a $\frac{dm}{dt} \Delta t$ che è la sabbia che cade sulla bilancia nel tempo $\Delta t$.
$\frac{1}{2} \frac{dm}{dt} \Delta t v_f^2 -\frac{1}{2} \frac{dm}{dt} \Delta t v_0^2 = \frac{dm}{dt} \Delta t gh$
(all'inizio in alto la sabbia, trascinata dal rullo, ha velocità verso il basso $v_0$).
Quindi la velocità finale è pari a:
$\sqrt(2gh+v_0^2)$
Per fermare la sabbia la bilancia nel tempo $\Delta t$ deve fornire una quantità di moto pari a
$\frac{dm}{dt} \Delta t \sqrt(2gh+v_0^2)$
quindi nell'unità di tempo sarà:
$\frac{dm}{dt} \sqrt(2gh+v_0^2)$
3) A questo punto il peso indicato dalla bilancia sarà dato dal peso della sabbia $M$ accumulato fino a quel momento più la forza che la sabbia esercita sulla bilancia per fermarsi pari alla variazione di quantità di moto nell'unità di tempo.
$Mg+\frac{dm}{dt} \sqrt(2gh+v_0^2)$