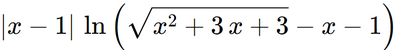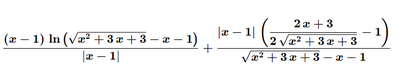[Risolto] Problema studio della monotonia di una funzione

Ciao sono appena rientrato in casa.
Sono riuscito oggi mentre ero a lavoro, nei ritagli di tempo, a provare a scrivere un qualcosa di sensato per spiegarti la mia idea (sperando di non aver commesso errori grossolani 😉 ).
Mi dispiace se è un po' disordinato e poco formale, ma non sono riuscito a fare di meglio.
Fammi sapere se ci capisci qualcosa, semmai poi proviamo a ripensarci insieme.

Detto questo: io non mi sono messo a calcolare la derivata seconda di tutta la funzione (ma solo di una parte), ma credo che forse alla fine diverse cose si sarebbero semplificate e sarebbe stato tutto più "formale e lineare"... Comunque questa è solo una supposizione.

In ogni caso ti carico i miei appunti, fammi sapere.

P.S. non ho trovato la X del punto di minimo, ho solo dimostrato che c'è UN SOLO PUNTO DI MINIMO tra -1 ed 1, quindi in realtà il risultato è comunque parziale.

Buongiorno,

anche questa è abbastanza impegnativa 🙂
Come la precedente, proviamo ad affrontarla un po' alla volta, perché purtroppo sono esercizi che richiedono di starci sopra, e il tempo a disposizione è quello che è...
Provo a darci un occhio e ti dico (considera però che stamani ho lezione e poi ho corsi di recupero fino alle 16.00, quindi non credo di riuscire a guardare molto presto).

A dopo.

Conviene usare la regola del prodotto 

h'=f' g + g' f

per dedurre dove h' è negativa nei tre intervalli

x<  - 1, - 1< x< 1, x > 1

studiando segno e crescenza dei due fattori, per il secondo solo l'argomento. 

Ciao,
Seguendo anche il consiglio di EidosM, intanto io proverei a guardare cosa succede per x<-1
Il Logaritmo dovrebbe risultare sempre positivo (prova ad impostare "argomento del log" >1).
Quindi in x<-1 il primo addendo della derivata prima risulta sempre negativo.

Guardiamo invece il secondo addendo.
Il Valore assoluto è sicuramente positivo in x<-1
Anche in denominatore è sicuramente positivo in x<-1 (radice sempre positiva e -x-1>0 <=> x<-1)
Resta da vedere l'altro fattore al numeratore cosa fa: ma anche quello con una semplice disequazione, vedi che è sempre negativo.

In definitiva per x<-1 di sicuro la derivata prima è negativa e quindi la funzione decrescente (spero che la fretta non mi abbia fatto prendere qualche abbaglio).

Restano gli altri due intervalli: io credo che suddividendo in "sottoproblemi" come fatto sopra, si possa arrivare a capire.

Scusa se rispondo in maniera frammentaria, ma davvero non è semplice stare dietro a tutto: comunque seguo.

Buongiorno,

purtroppo non sono riuscito a dedicarmi, però forse un'idea:
si riesce a studiare derivata prima=0 tra -1<x<1 in qualche modo ?
non mi sembra facile facile, ma forse ci si fa... ad esempio (x-1) e |x-1| al primo addendo si semplificano e lasciano un - ... magari ci sono altre semplificazioni che si riescono a fare, ma che al volo non sto vedendo.

Con questa info e poi cercando dei valori della derivata in modo empirico, forse si arriva.

Ciao,

questo esercizio mi pare un po'complicato onestamente (considera comunque che solitamente non mi cimento con esercizi di questo tipo, quindi ci sta che sia io "fuori allenamento").
Mi potresti dire cosa dice esattamente il testo?

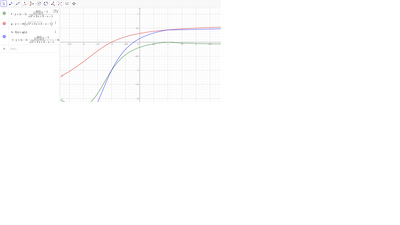
Considerando che sia in x=-1 che in x=1 la funzione vale 0, per il Teorema di Rolle all'interno di questo intervallo abbiamo di sicuro almeno un punto con derivata 0.
Calcolando f(-1/2) ed f(1/2) ad esempio si capisce che di sicuro c'è almeno un minimo (dato che entrambi restituiscono valori negativi).
Quindi la conclusione è che tra -1 ed 1 la funzione non è monotona di sicuro!

MA da qui a trovare gli intervalli di monotonia tra -1 ed 1, il passo mi pare lungo...
Ho provato a risolvere la derivata prima = 0 e non dico sia impossibile, ma mi sembra abbastanza complicato da scartare l'ipotesi che quella sia la strada.

Forse si può riuscire a dimostrare che nell'intervallo [-1, 1] non ci sono altri punti stazionari oltre al minimo di cui sopra:
dato che |x-1| è sempre decrescente in quell'intervallo ed è sempre positiva ed anche il logaritmo è sempre decrescente in quell'intervallo (si vede studiando il segno della derivata, questo è abbastanza semplice), ma è sempre negativo, credo si possa riuscire a concludere che non ci possa essere più di un minimo nell'intervallo (però, per ora, non sono riuscito a formalizzarlo).
Insomma se ci fossero almeno due minimi, la curva dovrebbe "tornare su e giù" 2 o 3 volte, e visto che |x-1| è lineare e anche il logaritmo in quell'intervallo "non fa giri strani", penso che in qualche modo si possa arrivare a confermare questa ipotesi...

Però per dire con esattezza quali sono gli intervalli di monotonia bisogna per forza (almeno credo) trovare le soluzioni di "derivata = 0" e, come dicevo, mi sembra un po' strano che un esercizio chieda di risolvere un calcolo di quel tipo... Quindi o c'è qualcosa a livello di calcolo che ci sta sfuggendo, per cui trovare le soluzioni di questa equazione, alla fine è più semplice di quello che sembra a noi (e non lo escludo) oppure per rispondere all'esercizio basta dire che tra -1 ed 1 la funzione non è monotona.

Comunque ci sta che mi stia sbagliando, eh, queste sono le mie ipotesi ad ora...
Se ci fosse qualcuno in ascolto con una soluzione, mi farebbe piacere sentirla, a questo punto mi sono incuriosito 🙂

P.S. nel tempo che ho dedicato, non ho ricontrollato la derivata onestamente, ho dato per scontato che quella che hai scritto fosse corretta e, a occhio, mi parrebbe di sì.

Buongiorno.
Sì, io avevo calcolato f(-1/2) ed f(1/2) perché la forma algebrica di "f" era più semplice di quella di "f primo" e mi risultava più immediato. Va benissimo ragionare come hai fatto tu sulle derivate prime, per concludere che c'è almeno un minimo.

E' una buona idea quella di calcolare la derivata seconda e accertarsi che non ci siano cambi di concavità, in questo modo ci garantiamo la "non esistenza di flessi e di massimi".
Unica piccola precisazione, se c'è un minimo, la concavità è rivolta verso l'alto 😉
Ho paura che "f secondo" possa venire un po' incasinato, ma magari siamo fortunati e qualcosa si semplifica.

seguo...

Un'altra strada che mi è venuta in mente è provare a dimostrare che il secondo addendo della derivata prima sia sempre decrescente nell'intervallo [-1, 1].

Non con la derivata seconda, ma in altri modi: ad esempio, se riesci a dimostrare che il numeratore è sempre decrescente e il numeratore sempre crescente, ottieni il risultato anche senza la derivata seconda.
Puoi provare a sfruttare informazioni "empiriche", tipo che il vertice della parabola sotto radice al denominatore ha vertice in x=-3/2 (quindi da lì verso destra il radicando è crescente di sicuro).
Ora sono un po' incasinato, ma se si riesce a dimostrare questo, siamo a posto (prova a capire da solo perché, ma appena ho un po' più di tempo, semmai, provo a spiegartelo).

Ciao,

scusami, prima avevo preso un abbaglio (capita)... 
Dato che in [-1, 1] il primo addendo della derivata è positivo crescente (questo è vero, visto che il logaritmo è negativo decrescente e gli altri due termini, semplificandosi, lasciano "un segno meno"), se l'altro addendo fosse stato negativo decrescente, si poteva tranquillamente concludere che che se c'era una "x" in cui la loro somma faceva 0, non ce ne potevano essere altre (cioè, mi sembrava si potesse trarre questa conclusione, ma mi sbagliavo).
Purtroppo non è così: ho ceduto "alla tentazione" e ho provato a metterlo su Geogebra per vedere effettivamente il comportamento... C'è solo punto in cui la loro somma fa 0, in effetti, ma sono entrambi crescenti (vedi immagine).

Purtroppo lavorandoci "a intermittenza" in questo modo, non riesco a trovare una soluzione (e non sono sicuro di riuscire a trovarla nemmeno potendomici dedicare con maggior tempo e concentrazione), mi spiace.

Prova a ripostare la domanda, vediamo se qualcuno viene in aiuto (semmai tienimi aggiornato 🙂 ).
Comunque, secondo me, dire che tra -1 ed 1 non è monotona, già non è poco...

Vedi la stanchezza...
Ripensandoci a mente lucida stamani, proprio perché sono entrambe crescenti (una positiva ed una negativa) siamo tranquilli che se la loro somma si annulla in un punto, allora si annulla solo in quel punto.

Bisognerebbe quindi dimostrare che il secondo addendo è sempre crescente... Ma risiamo lì...
Se mi mandi il calcolo della derivata del secondo addendo, posso provare a vedere se si riesce a trarre questa conclusione.

Penso di aver trovato la soluzione.

Nel tardo pomeriggio (quando rientro a casa da lavoro) provo a formalizzarla e girartela. 

Te lo rimando in PDF, che in PNG mi sa che si legge male

Sì, in effetti il documento è un po' caotico, mi rendo conto. Se vuoi, fammi sapere dove ti blocchi o non ti torna... Comunque son sicuro che ci sia una strada migliore di questa, che forse conduce anche a trovare esattamente il punto di minimo (e penso che passi dalla derivata seconda).
Quindi vedi tu se è il caso di ripostare la domanda...