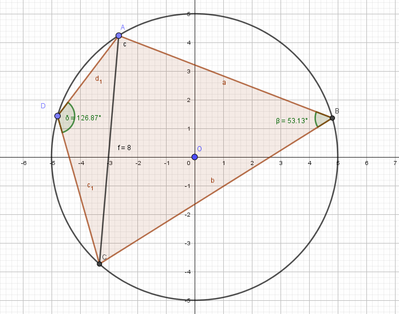
Il quadrilatero $A B C D$ e inscritto in una circonferenza di raggio 5 e $\overline{A C}=8$. Calcola seno e coseno degli angoli $\widehat{B}$ e $\widehat{D}$ supponendo che il vertice $B$ si trovi sul maggiore dei due archi di estremi $A$ e C.
$$
\left\lceil\sin \widehat{B}=\frac{4}{5} ; \cos \widehat{B}=\frac{3}{5} ; \sin \widehat{D}=\frac{4}{5} ; \cos \widehat{D}=-\frac{3}{5}\right]
$$
Potete darmi una mano con questo problema?
45
punti
Livello 0
Ciao.
Il teorema della corda in geometria piana, stabilisce che la lunghezza di una corda AC di una circonferenza di raggio r è data dal doppio prodotto del raggio per il seno di uno degli angoli alla circonferenza che insistono sulla corda.
In formule: AC = 2·r·SIN(β) = 2·r·SIN(δ)
Con riferimento alla figura allegata:
SIN(β)=AC/2·r = 8/10=4/5 (angolo acuto: β = 53.13)
SIN(δ) =4/5 (angolo ottuso:δ = 126.87)
COS(β) = √(1 - (4/5)^2) =COS(β) = 3/5 ; COS(δ) = - 3/5
96630
punti
Genius II
Ma certo che posso! Che sondaggio è? Si vince qualcosa?
57400
punti
Genius I
