Salve a tutti, sto provando a risolvere questo esercizio tratto da un vecchio tema d'esame di fisica 1.
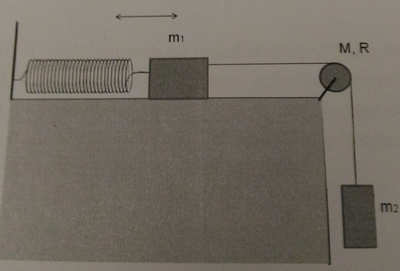
Un blocco di massa m1 = 4kg è poggiato su un piano orizzontale liscio ( nessun attrito) ed è connesso a sinistra con l'estremità di una molla ideale , di costante k = 300 N/m, fissata per l'altra estremità ad un supporto fisso, e a destra da un filo inestensibile ideale. Tale filo è parzialmente avvolto su una carrucola ideale di massa M = 0,2 kg e raggio R = 20 cm ed è connesso ad una seconda massa m2 = 6 kg, verticalmente sospesa ad esso. Si consideri il sistema in equilibrio statico
1) Si determini l'allungamento della molla all'equilibrio
Si supponga che adesso la massa m2 venga spostata verso il basso, a partire dalla posizione di equilibrio, di h = 3 cm e quindi lasciata andare da ferma ( istante t = 0). Supponendo che non ci sia slittamento tra filo e carrucola e che questa possa ruotare intorno al suo centro senza attrito:
2) Si dimostri che il moto del sistema è armonico e se ne calcoli il periodo ( momento di inerzia della carrucola è I =(1/2)MR^2)
3) Si determinino, nell'istante iniziale t=0, le tensioni del filo a sinistra e a destra della carrucola e l'accelerazione di m1
4) la velocità e l'accelerazione massima della carrucola.
Per il primo punto ho applicato le leggi della dinamica alle due masse e alla carrucola e ho trovato che l'allungamento x vale circa 19,6 cm.
Riguardo al punto 3 pensavo di applicare questo sistema di equazioni:
T1 - k(x+h) = m1 a
m2 g - T2 = m2 a
T1*R -T2*R = I*a/R
Qualcuno può aiutarmi ?