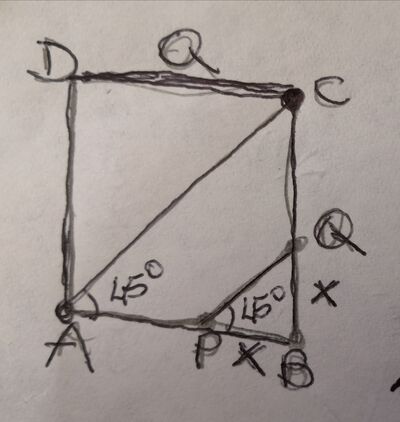
Sia ABCD un quadrato il cui lato misura a e P un punto sul lato AB. La retta passante per P e parallela alla diagonale AC incontra il lato BC in Q. Determina la misura di AP in modo che l'area del pentagono APQCD sia il triplo dell'area del triangolo PQB.
Grazie mille in anticipo.
109
punti
Livello 1
Essendo PQ // AC il triangolo PQB è un triangolo rettangolo isoscele.
Posto: PB= x ; 0< x < a
L'area del pentagono risulta essere la differenza tra l'area del quadrato e quella del triangolo PQB.
Avendo il quadrato area a², imponendo la condizione richiesta, il pentagono avrà area (3/4)*a² e il triangolo rettangolo isoscele area (1/4)*a²
Quindi:
(1/2)*x² = (1/4)*a²
(Area triangolo rettangolo isoscele)
Da cui si ricava l'unica soluzione accettabile:
x=a*radice (2)/2
Essendo PB=x
AP = a - PB = a* [1 - (radice (2)/2)]
75827
punti
Genius II
