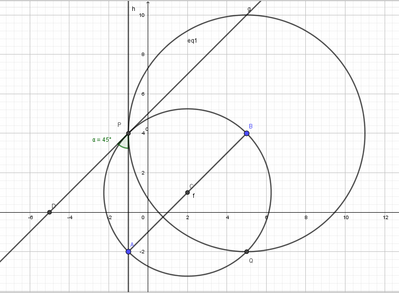
Il diametro AB, di estremi A(- 1, - 2) e B(5, 4), ha
* punto medio C(2, 1)
* lunghezza 2*r = 6*√2 ≡ r = 3*√2 ≡ r^2 = 18
quindi la circonferenza alfa è
* α ≡ (x - 2)^2 + (y - 1)^2 = 18 ≡
≡ x^2 + y^2 - 4*x - 2*y - 13 = 0
------------------------------
La circonferenza beta
* β ≡ x^2 + y^2 - 10*x - 8*y + 5 = 0 ≡
≡ x^2 - 10*x + y^2 - 8*y + 5 = 0 ≡
≡ (x - 5)^2 - 25 + (y - 4)^2 - 16 + 5 = 0 ≡
≡ (x - 5)^2 + (y - 4)^2 = 6^2
ha
* centro K(5, 4)
* raggio R = 6 > r = 3*√2 ~= 4.24
NOTA
Un quadrato costruito su R ha diagonale 2*r.
==============================
OTTEMPERANZA ALLE CONSEGNE
------------------------------
1) "verifica che ... con P nel secondo quadrante"
---------------
1a) "calcola ... P e Q, con P nel secondo quadrante"
* α & β ≡ ((x - 2)^2 + (y - 1)^2 = 18) & ((x - 5)^2 + (y - 4)^2 = 36) ≡
≡ P(- 1, 4) oppure Q(5, - 2)
Il segmento PQ è lungo 6*√2 e giace sulla y = 3 - x.
Quindi è un diametro di α (2*r = 6*√2), e la diagonale del quadrato del raggio di β (R = 6).
---------------
1b) "verifica che α e β sono secanti"
Sub 1a si sono prodotte due intersezioni reali e distinte.
------------------------------
2) "determina le equazioni ... angolo acuto formato da esse"
---------------
2a) "determina le tangenti in P" ad α e β
Per sdoppiamento rispetto a P(- 1, 4) sulle forme normali canoniche si ha
* da α ≡ x*(- 1) + y*(4) - 4*(x - 1)/2 - 2*(y + 4)/2 - 13 = 0 ≡ y = x + 5
* da β ≡ x*(- 1) + y*(4) - 10*(x - 1)/2 - 8*(y + 4)/2 + 5 = 0 ≡ x = - 1
---------------
2b) "calcola l'ampiezza dell'angolo acuto formato da esse"
Non occorre calcolare nulla: una parallela all'asse y e una parallela alla bisettrice dei quadranti dispari formano un angolo acuto di π/4 = 45°.
------------------------------
3) "verifica che α passa per il centro di β e determina le aree delle partizioni del cerchio di β divise dall'arco secante di α"
---------------
3a) "α passa per il centro K(5, 4) di β?"
Sì, PQ è un diametro di α; e comunque
* da α ≡ (5 - 2)^2 + (4 - 1)^2 = 18 ≡ 3^2 + 3^2 = 18 ≡ VERO
---------------
3b) "determina le aree delle partizioni del cerchio di β divise dall'arco secante di α"
* area del cerchio S(C) = area della lunula S(L) + area della differenza S(D)
--------
Qui entrano in ballo le osservazioni sulle relazioni fra r, R e |PQ|: la corda PQ è lunga quanto il diametro di α (2*r = 6*√2) e la diagonale del quadrato del raggio di β (R = 6).
3b1) Ne segue che la lunula suddivisa nel cerchio di α dall'arco secante di β è una "Lunula di Ippocrate" di area A pari a un quarto del quadrato di diagonale 2*r
* A = (2*r/√2)^2/4 = (2*r/√2)^2/4 = r^2/2 = 9.
3b2) Ne segue che S(D) = (π - 1/2)*r^2 = 18*(π - 1/2)
3b2) Ne segue che la lunula grande ha area S(L) = S(C) - S(D) =
= π*R^2 - 18*(π - 1/2) =
= 36*π - 18*(π - 1/2) = 9*(1 + 2*π)
--------
Risposta
* area della lunula S(L) = 9*(2*π + 1)
* area della differenza S(D) = 9*(2*π - 1)