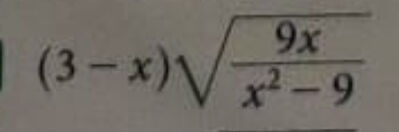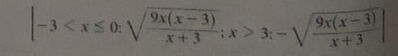[Risolto] Portare dentro una radice di indice pari

@sara987, questa la mia spiegazione:

LE PAROLE SONO IMPORTANTI!
------------------------------
TIPOLOGIA
– 1. Suddivisione, distribuzione e classificazione di una molteplicità di individui, oggetti, fatti, elementi e fattori, omogenei o similari, in gruppi caratterizzati dall'appartenenza a determinati tipi formali e funzionali.
---------------
Gli esercizi scolastici si suddividono in poche tipologie ben distinte.
* Esercizi di lingue classiche (greco, latino, raramente altre).
* Esercizi di lingue moderne (italiano, inglese, ...).
* Esercizi di altre materie umanistiche (storia, filosofia, pedagogia, ...).
* Esercizi di materie scientifiche (matematica, fisica, statistica, ...)
* Esercizi di materie tecniche (disegno, informatica, meccanica, ...)
* Esercizi di ... e così via.
Nella tipologia "Esercizi di materie scientifiche" si distinguono gruppi caratterizzati dall'appartenenza alle singole materie.
Nella tipologia "Esercizi di materie scientifiche", nel gruppo "Esercizi di matematica" si distinguono sottogruppi caratterizzati dall'appartenenza alle singole branche della materia (aritmetica, geometria euclidea, teoria delle categorie, ...).
E GIU' GIU' RAMIFICANDO LA TASSONOMIA FINO A COGLIERE "Esercizi di questo TIPO".
==============================
La funzione
* y = f(x) = (3 - x)*√(9*x/(x^2 - 9))
per x < - 3 ha valori immaginarii
per x = - 3 non ha valore essendo indefinita
per - 3 < x < 0 ha valori reali positivi
per x = 0 vale zero
per 0 < x < 3 ha valori immaginarii
per x = 3 non ha valore essendo indefinita
per x > 3 ha valori reali negativi
NB: ha un solo asintoto verticale in x = - 3, perché
* lim_(x → 3) f(x) = 0
------------------------------
Incorporare nel radicando il fattore esterno alla radice comporta il doppio segno mostrato nel risultato atteso in base alla distruzione d'informazione dovuta alla potenza d'esponente pari
* √(a^2) = |a| = ± a
---------------
Nei due intervalli di realtà della y = f(x) si ha
* in - 3 < x < 0: (3 - x) > 0 →
→ (3 - x)*√(9*x/(x^2 - 9)) = √(9*x*(3 - x)^2/(x^2 - 9)) =
= √(9*x*(x - 3)/(x + 3))
* in x > 3: (3 - x) < 0 →
→ (3 - x)*√(9*x/(x^2 - 9)) = - (x - 3)*√(9*x/(x^2 - 9)) =
= - √(9*x*(x - 3)^2/(x^2 - 9)) =
= - √(9*x*(x - 3)/(x + 3))
MA SI PUO' ANCHE VEDERLA IN MODO PIU' GREZZO
* y = f(x) = (3 - x)*√(9*x/(x^2 - 9)) =
= √(9*x*(3 - x)^2/(x^2 - 9)) =
= ± 3*√(x*(x - 3)/(x + 3))