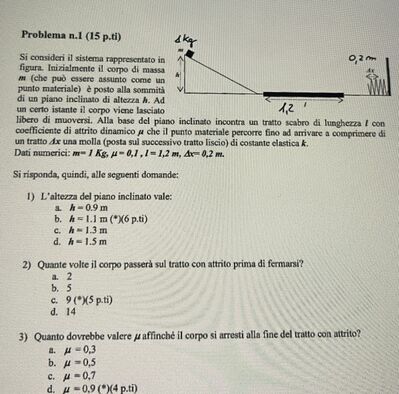
Problema n.1 (15 p.ti) $\quad$ \& $k$ g
Si consideri il sistema rappresentato in figura. Inizialmente il corpo di massa $m$ (che può essere assunto come un punto materiale) è posto alla sommità di un piano inclinato di alterza $h$. Ad un certo istante il corpo viene lasciato
libero di muoversi. Alla base del piano inclinato incontra un tratto scabro di lunghezza $l$ con coefficiente di attrito dinamico $\mu$ che il punto materiale percorre fino ad amivare a comprimere di un tratto $d x$ una molla (posta sul successivo tratto liscio) di costante clastica $k$.
Dati numerici: $m=1 Kg , \mu=0,1, l=1,2 m, \Delta x=0,2 m$.
Si risponda, quindi, alle seguenti domande:
1) L'altemza del piano inclinato vale:
a. $h=0.9 m$
b. $h=1.1 m \left({ }^*\right)(6 p . i )$
c. $h=1.3 m$
d. $h=1.5 m$
2) Quante volte il corpo passerá sul tratto con attrito prima di fermarsi?
a. 2
b. 5
c. $9\left(^*\right)(5$ p.ti)
d. 14
3) Quanto dovrebbe valere $\mu$ affinché il corpo si arresti alla fine del tratto con attrito?
a. $\mu=0,3$
b. $\mu=0,5$
c. $\mu=0.7$
d. $\mu=0.9(*)(4$ p.ti)
salve, ho fatto alcune considerazioni al riguardo ma non riesco a svolgere l’esercizio.
Inizialmente il corpo possiede una certa energia potenziale (essendo fermo) pari a mgh. Tale energia si trasforma in energia cinetica quando il corpo viene messo in moto. Avevo anche considerando che il piano alla base del piano inclinato, essendo scabro, dissipa una certa quantità di energia, compiendo un lavoro. Per conoscere l’energia cinetica finale (quella con cui il corpo andrà a comprimere la molla) dovrei sottrarre, alla energia cinetica iniziale, l’energia dissipata.