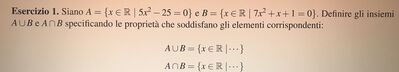Esercizio 1. Siano $A=\left\{x \in R \mid 5 x^2-25=0\right\}$ e $B=\left\{x \in R \mid 7 x^2+x+1=0\right\}$. Definire gli insiemi $A \cup B$ e $A \cap B$ specificando le proprietà che soddisfano gli elementi corrispondenti:
$$
\begin{array}{l}
A \cup B=\{x \in R \mid \cdots\} \\
A \cap B=\{x \in R \mid \cdots\}
\end{array}
$$
127
punti
Livello 1
x²-5=0 => x=± radice (5)
7x²+x+1=0 => non esistono x€R
Quindi:
A= {±radice 5}
B= ∅
A U B = A
A ∩ B = ∅
76643
punti
Genius II
Contesto vivamente l'uso del sintagma "elementi corrispondenti": per avere corrispondenza occorre definire una funzione da un insieme all'altro oppure due ordinamenti totali che consentano la banale corrispondenza "a pari posizione"; ma fra le proprietà associate al concetto di "insieme" c'è, oltre all'unicità degli elementi, anche l'assenza di relazioni fra di essi.
---------------
A parte la terminologia infelice, l'esercizio definisce due insiemi per proprietà caratteristica: essere zeri reali di un dato bi/trinomio quadratico (A due valori opposti; B nessuno) e chiede, con i puntini d'ellissi, di formulare la proprietà caratteristica di "A ∪ B" (la stessa di A) e di "A ∩ B" (la stessa di B).
Almeno a me, la richiesta "specificando ... elementi corrispondenti", risulta incomprensibile.
57171
punti
Genius I
