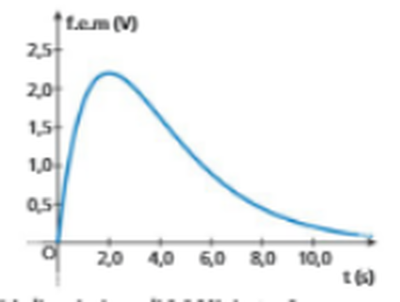
Il grafico rappresenta l’andamento della f.e.m. indotta in funzione del
tempo.
a. Indica, motivando la risposta, quale delle seguenti funzioni descrive la f.e.m.
indotta rappresentata in figura.
f(t) = At (e^(-t/τ)+ B) ; g(t) = Ate^(-t/τ)
b. Verificato che la funzione cercata è g(t), determina i valori di A e τ, specificando
le relative unità di misura, sapendo che la f.e.m. raggiunge il suo valore massimo
dopo 2,0 s e ha una velocità di variazione di 3,0 V/s in t = 0.
c. Considera la funzione φ(t) che rappresenta il flusso del campo
elettromagnetico. Puoi affermare che φ(t) è monotòna? E che ha un asintoto
orizzontale?