Nel grafico è rappresentata la funzione $f(x)=e^{\frac{x+k}{x}}$.
a. Trova il valore di $k$.
b. Determina il dominio e l'insieme immagine di $f(x)$ e individua gli intervalli in cui è crescente.
c. Indica se è invertibile e trova l'espressione analitica della funzione inversa.
Aiuto per favore, come devo fare? va bene anche una semplice spiegazione. Grazie mille💖
32
punti
Livello 0
Ho completato la risposta. Dacci un'occhiata.
Quale esercizio?
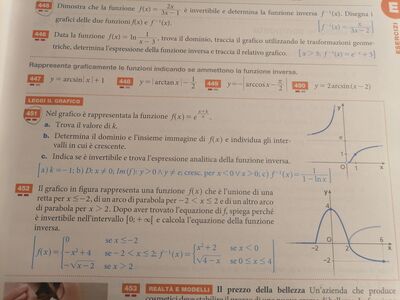
Ex 451
y = e^((x + k)/x)
determino k imponendo il passaggio per il punto di figura:
1 = e^((1 + k)/1)--> k = -1
Quindi la funzione è:
y = e^(1 - 1/x)
per cui il C.E. è:
]-∞,0[ ∪ ]0,+∞[
le condizioni agli estremi sono:
LIM(e^(1 - 1/x)) =e
x---> -∞
LIM(e^(1 - 1/x)) =e
x---> +∞
che indicano asintoto orizzontale y = e
come illustrato nella figura allegata al testo
Gli altri due limiti:
LIM(e^(1 - 1/x)) =+∞
x---> 0-
LIM(e^(1 - 1/x)) = 0
x---> 0+
(indicano discontinuità di 2^ specie)
Insieme immagine:
y>0 con y ≠ e
-------------------------------------------
y'= dy/dx =e^(1 - 1/x)/x^2
sempre crescente e non definita per x =0
e^(1 - 1/x)/x^2 > 0----> true
------------------------------------------
funzione inversa:
per def: 1 - 1/x = LN(y)----> x = 1/(1 - LN(y))
Funzione inversa: y = 1/(1 - LN(x))
96624
punti
Genius II
@lucianop Mi scusi, ha ragione. Mi è sfuggito il numero: è il 451.
