Salve, ho una domanda. Riesco tranquillamente a calcolare il minimo ed il massimo di una funzione e a trovare crescenza e decrescenza.
Ma per trovare la coordinata y del punto di minimo (o massimo) non ho capito se devo sostituire nella y o nella y'.
Stessa cosa per la sostituzione nel flesso (sostituisco nella y o nella y''?).
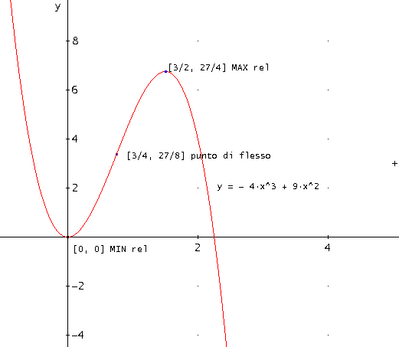
ESEMPIO: y=-4x^3+9x^2
Ho trovato x=0 minimo e x=3/2 massimo ma non so qual è la coordinata y.
Poi ho trovato x=3/4 flesso ma non sono sicura lo sia. Come faccio a stabilirlo con certezza?
Grazie a tutti