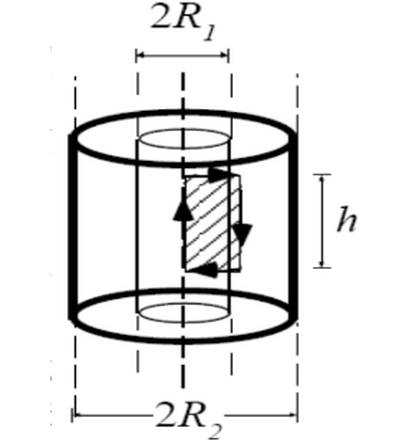
Un conduttore cilindrico rettilineo cavo, di raggio R1, da considerarsi infinitamente lungo, è circondato da una buccia cilindrica coassiale, anch'essa infinitamente lunga, di raggio R2 > 2R1. Gli spessori delle pareti dei due conduttori sono trascurabili. Sulla superficie del conduttore interno scorre uniformemente una corrente I, diretta verso il basso. Sulla superficie del conduttore esterno scorre uniformemente la stessa corrente I, diretta in verso opposto. Nel caso in cui la corrente sia continua, I = I0, si chiede:
i) L'espressione di B (modulo, direzione e verso) in tutto lo spazio.
Una spira rettangolare di altezza h e lato L = 1.1 R1 (area tratteggiata in figura) è posta con l'altezza coincidente con l'asse del conduttore interno, mentre il lato è diretto radialmente. L'orientazione è come in figura. Nel caso in cui la corrente cresca linearmente nel tempo, I = k t, si chiede:
ii) la f.e.m. indotta nella spira.
(I0 = 6.3 A; R1 = 2.5 mm; h = 5 mm; k = 7.3 A/s; m0=4p*10-7Tm/A)