@mirea00
Ciao. Riscrivo il testo:
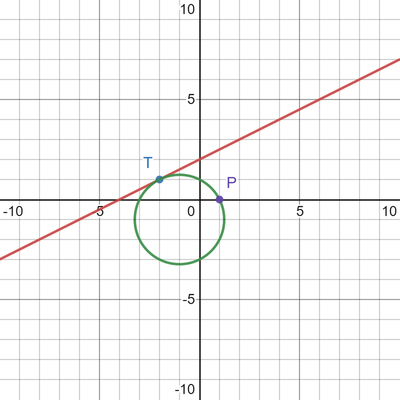
Determina l'equazione della circonferenza tangente alla retta di equazione x-2y+4=0 nel suo punto di ascissa -2 e passante per P(1;0)".
Determino il punto di tangenza A inserendo la sua ascissa nell'equazione della tangente:
-2 - 2·y + 4 = 0---->y = 1 quindi A(-2,1)
Esplicito la retta tangente: y = x/2 + 2 (m'=1/2)
Il centro della circonferenza C sta su una retta perpendicolare a questa con coefficiente angolare pari a
m=-2. Determino quindi tale retta.
y = - 2·x + q per A(-2,1)------> 1 = - 2·(-2) + q----->1 = q + 4---> q = -3
Quindi: y = - 2·x - 3
Il centro della circonferenza deve avere coordinate pari a C(x,- 2·x - 3)
Impongo quindi l'equidistanza di C da A(-2,1) e da P(1,0): CA = CP
Quindi:
√((-2 - x)^2 + (1 - (- 2·x - 3))^2) = √((1 - x)^2 + (0 - (- 2·x - 3))^2)
elevo al quadrato:
(x^2 + 4·x + 4) + (4·x^2 + 16·x + 16) = (x^2 - 2·x + 1) + (4·x^2 + 12·x + 9)
sviluppo:
5·x^2 + 20·x + 20 = 5·x^2 + 10·x + 10
Risolvo:
x = -1
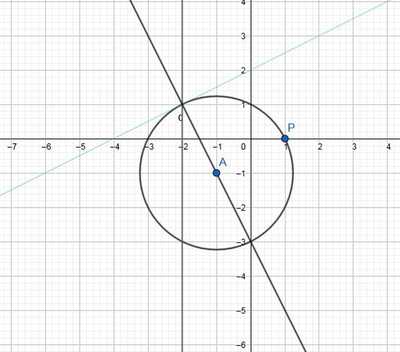
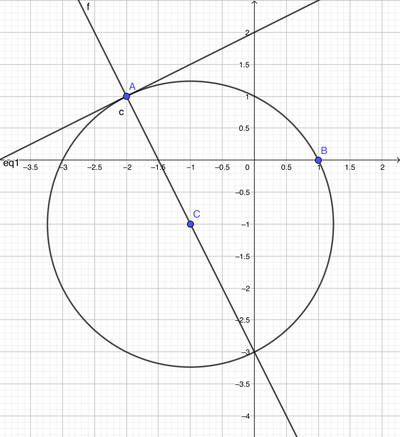
Centro C della circonferenza: x=-1----->y=- 2·(-1) - 3=-1---->C(-1,-1)
raggio della circonferenza:
√((-2 - (-1))^2 + (1 - (- 2·(-1) - 3))^2) =√5
Equazione cartesiana: (x + 1)^2 + (y + 1)^2 = √5^2
Equazione implicita: x^2 + y^2 + 2·x + 2·y - 3 = 0