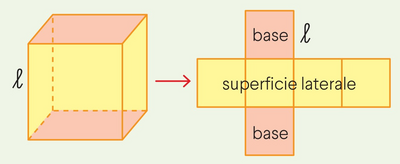
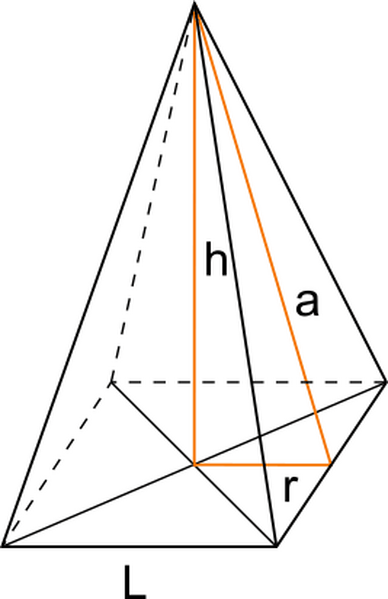
Un cubo ha l'area laterale di $676 dm ^2$. Una piramide regolare quadrangolare ha il perimetro di base uguale a 10/13 del perimetro di una faccia del cubo. Calcola il volume della piramide, sapendo che il suo apotema è uguale allo spigolo del cubo.
$\left[400 dm ^3\right]$
10
punti
Livello 0
chiedi di risolvere il 400 e posti il testo del 385 : ci sei o ci fai?🤭
cubo
area laterale AL = ℓ^2*4 = 676
spigolo ℓ = √676/4 = √169 = 13 cm
perimetro di una faccia 2p = 4ℓ = 13*4 = 52 cm
piramide quadrangolare (ha per base un quadrato)
perimetro di base 2p'= 2p*10/13 = 52/13*10 = 40 cm = 4L
lato L = 2p'/4 = 40/4 = 10 cm
r = L/2 = 10/2 = 5 cm
apotema a = ℓ = 13 cm
altezza h = √a^2-r^2 = √13^2-5^2 = √144 = 12 cm
volume V = L^2*h/3 = 10^2*12/3 = 100*4 = 400 cm^2
96649
punti
Genius II
