Heyo, ho un dubbio su questa disequazione: $\frac{7-x^2}{\sqrt{x+\sqrt{5}}}≥ :0$
Si avrà per il numeratore: $-\sqrt{7}≤ x ≤\sqrt{7}$
Per il denominatore: $x>- 5$
Ecco il grafico dei segni che ho fatto:
La soluzione della disequazione è $- \sqrt{5}≤x≤\sqrt{7}$
Perché $x ≤ - \sqrt{7}$ non viene considerato? Dove sbaglio?
Grazie 🖐️
758
punti
Livello 1
Avevo quasi dimenticato che editando, LaTex impazzisce... 😒
** Per il denominatore si avrà: $x>-\sqrt{5}$
Non posso editare se no saltano tutti i codici 😣
*** Il risultato della disequazione è $-\sqrt{5}\le x\le \sqrt{7}$, qualcosa è andato ulteriormente storto nel codice lassù.
@iloveyou sistemato 😁
SOLUZIONE
$\frac{7-x^{2}}{\sqrt{x+\sqrt{5}}}\geq0$
Scriviamo le condizioni di esistenza
$x+\sqrt{5}<0~\Rightarrow~x<-\sqrt{5}$
$\sqrt{x+\sqrt{5}}=0~\Rightarrow~x=-\sqrt{5}$
$x\in(-\infty,~-\sqrt{5}]$
$x\in(-\sqrt{5},~+\infty)$ cioè $x\geq-\sqrt{5}$
Poiché il denominatore è sempre positivo (dopo aver posto le $C.E.$), determiniamo ora quando il numeratore è $geq0$
$7-x^{2}\geq0$
$-x^{2}\geq-7$
$x^{2}\leq7$
$|x|\leq\sqrt{7}$
$-\sqrt{7}\leq{x}\leq\sqrt{7}$
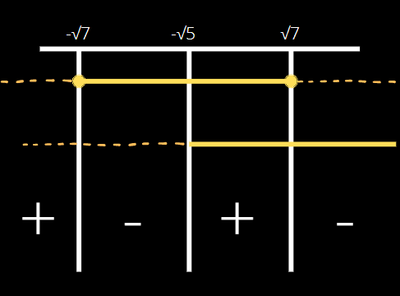
Troviamo infine l'intersezione fra soluzione e condizioni di esistenza
$\begin{cases}-\sqrt{7}\leq{x}\leq\sqrt{7}\\x\geq-\sqrt{5}\end{cases}~\Rightarrow~-\sqrt{5}<x\leq\sqrt{7}$
3594
punti
Livello 5
@ILoveYou, dammi qualche minuto per sistemare la risposta 😅😢.
@SosMatematica, c’è un problema con il codice LateX.
@us sto cercando di decifrare nel mentre 😆
@us in realtà non mi è molto chiaro come hai posto le CE.
Io ho semplicemente calcolato $\sqrt{x+\sqrt{5}}\ne 0$ trovando $x\:\ne -\sqrt{5}$.
Forse non mi è chiaro perché non ho ancora studiato le disequazioni irrazionali? Questa disequazione era parte di un'equazione irrazionale 😱
@us L'equazione era $\sqrt{x-\sqrt{5}}=\frac{7-x^2}{\sqrt{x+\sqrt{5}}}$.
Mi son ritrovato a calcolare la CSS ed ho posto il secondo membro maggiore o uguale a zero.
Forse avrei potuto calcolare solo il numeratore $\ge 0$ essendo il denominatore sempre positivo tranne per $x\:\ne -\sqrt{5}$? (sempre se le CE si calcolino così 😆)
Ciao!
Dimentichi la condizione di esistenza sul radicale a denominatore.
Deve essere $ x>-\sqrt{5} $ (non prendi l' = in quanto il termine si trova a denominatore).
Ti trovi?
851
punti
Livello 2
@gabriele22 beh sì, non l'ho scritto. L'ho tenuta però a mente scrivendo $x>-\sqrt{5}$ come risultato del denominatore 🤔
@gabriele22 Cioè, aspetta. La CE è $x\:\ne \sqrt{5}$, il risultato del denominatore invece è $x>-\sqrt{5}$. Sì?
@gabriele22 Ho risolto. Grazie!
@ILoveYou Perfetto ahah. Scusami se non mi sono riconnesso prima😅
