Salve, ho un porblema con questo radicale doppio :
Devo trovare il valore naturale di 'x', poi dell'equazione.
Come faccio a togliere la 'x'?
Salve, ho un porblema con questo radicale doppio :
Devo trovare il valore naturale di 'x', poi dell'equazione.
Come faccio a togliere la 'x'?
Ciao @LucianoP , grazie della risposta. Questo è quanto è scritto nell'esercizio.
(3-2\sqrt{3})\sqrt{21+6\sqrt{x}}
Ti giro il link per vedere tu stesso.
https://it.openprof.com/wb/i_radicali_esercizio_142?ch=171
Sono riuscito a trovare la soluzione data dalla persona che ha creato il problema, grazie mille dell'aiuto @yuri_nardi e @lucianoP
Una volta trovato il valore di x, calcola il valore dell'espressione :
Per eliminare la radice, deve verificarsi che:
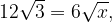
in modo da ottenere un prodotto corrispondente alla differenza di quadrati:
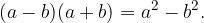
Il valore di x che ci consente di eliminare il segno di radice è:
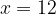
ad ogni modo entrambe le vostre soluzioni mi parevano corrette, quella di trovare il n^2 però mi era parsa troppo complessa per questo quesito.
Io nel mio piccolo commesi l'errore di ignorare la prima parentesi e considerando solo il radicando quando giustappundo non essendo una equazione non si può.
ciao, il ragionamento sembra essere corretto per la tua interpretazione della richiesta (attento al risultato finale dove devi scegliere -3 perché hai un prodotto tra fattori a segni discordi). per me è proprio quest'ultima ad essere ambigua e avrei posto il quesito diversamente per avere questa risoluzione.
L'ITALIANO E' ANCORA UNA LINGUA PER BENE, CON OGNI PAROLA CHE VALE CIO' CHE DICE IL DIZIONARIO?
Il testo originale è
«Trova il valore del numero naturale x tale da eliminare la doppia radice nell'espressione:
(3 - 2*√3)*√(21 + 6*√x)
Una volta trovato il valore di x, calcola il valore dell'espressione.»
e ciò vuol dire che si deve determinare un "numero naturale x" per cui l'espressione data ne valga una in cui "la doppia radice" (cioè "√(21 + 6*√x)") sia ELIMINATA (cioè non si veda più, diventi una subespressione "S" priva di radici).
Per soddisfare a tale consegna occorre E BASTA che:
* x sia un numero naturale quadrato perfetto, x = n^2;
* anche "21 + 6*n = 3*(7 + 2*n)" sia un numero naturale quadrato perfetto, 3*(7 + 2*n) = S^2;
dove (n, y) sono numeri interi relativi qualsiasi.
------------------------------
La soluzione si ottiene, per ogni k intero relativo non in {0, 1}, nei seguenti termini.
* S = - 3*(2*k - 1)
* S^2 = 9*(2*k - 1)^2
* n = 2*(3*(k - 1)*k - 1)
* x(k) = n^2 = 4*(3*((3*(k - 2)*k + 1)*k + 2)*k + 1)
La funzione x(k) ha
* un massimo relativo x(1/2) = (7/2)^2
* due minimi relativi e assoluti x(1/2 ± ~0.76) = 0
pertanto (a titolo d'esempio e per rispondere al secondo quesito) mostro di seguito, per i vicini dello zero di k, alcune triple dei valori {k, x(k), (3 - 2*√3)*√(21 + 6*√(x(k)))}.
{-5, 31684, 33*(3 - 2*√3)}
{-4, 13924, 27*(3 - 2*√3)}
{-3, 4900, 21*(3 - 2*√3)}
{-2, 1156, 15*(3 - 2*√3)}
{-1, 100, 9*(3 - 2*√3)}
{ 0, 4, (√33)*(3 - 2*√3)}
{ 1, 4, (√33)*(3 - 2*√3)}
{ 2, 100, 9*(3 - 2*√3)}
{ 3, 1156, 15*(3 - 2*√3)}
{ 4, 4900, 21*(3 - 2*√3)}
{ 5, 13924, 27*(3 - 2*√3)}
Mentre il caso di @LucianoP è
{1/√3, 12, - 3}
Devi trovare il valore di x che permette l’eliminazione del radicale doppio. Quindi porti sotto segno di radice 6 ed hai:
√(21 + √(36·x))
puoi trasformare questa espressione nella somma di due radicali quadratici, attraverso la formula del radicale doppio
√(r + √s) = √((r + q)/2) + √((r - q)/2)
se riesci a trovare un valore di q per cui risulta: r^2 - s = q^2
cioè q quadrato perfetto.
Nel tuo caso:
21^2-36x=q^2
Risolvo in x:
x = (441 - q^2)/36
x = 49/4 - q^2/36
Provo con q=2:x = 49/4 - 2^2/36------->x = 437/36 non è naturale: NON va bene
Provo con q=3: x = 49/4 - 3^2/36------> x = 12 OK!
Per x=12:
√(21 + √(36·12))= √(21 + √432)
quindi:
21^2 - 432 = 9------->q=3
√((r + q)/2) + √((r - q)/2)=√((21 + 3)/2) + √((21 - 3)/2) = 2·√3 + 3
Per tale valore di x
(3 - 2·√3)·√(21 + 6·√x)= (x=12) =(3 - 2·√3)·(2·√3 + 3) = -3
è il valore finale!
Infatti:
(3 - 2·√3)·√(21 + 6·√12) =-3
.
@lucianop Grazie, ma continuo a non capire la soluzione, o come procedere per trovare il quadrato perfetto di q.
...