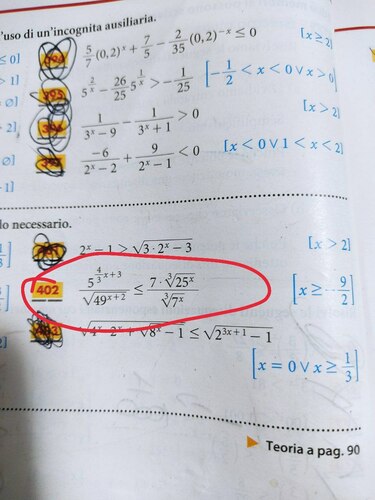Ciao a tutti, sto cercando di risolvere questa disequazione: $\displaystyle\frac{5^{\frac{4}{3}x+3}}{\sqrt{49^{x+2}}}\le \frac{7\cdot \sqrt[3]{25^x}}{\sqrt[3]{7^x}}$.
Ho fatto diversi tentativi di risoluzione, ma non sono mai riuscito ad arrivare alla soluzione, ovvero $x\ge -\frac{9}{2}$.
Il tentativo più promettente forse era questo:
$\displaystyle\frac{\sqrt[3]{5^{4x}}\cdot \:5^3}{\sqrt{7^{2x+4}}}\le \frac{7\cdot \sqrt[3]{5^{2x}}}{\sqrt[3]{7^x}}$.
Da qui però non so cosa fare, dividere le radici del numeratore? Togliere la radice nel primo denominatore? Non saprei, non si possono nemmeno effettuare sostituzioni avendo due basi differenti 😳
Qualcuno può indicarmi la retta via? 😂
Grazie in anticipo 🖐️