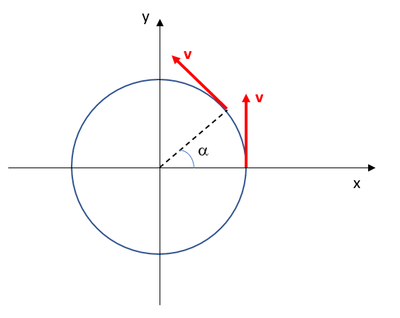
Un'automobile si muove su di una traiettoria circolare di raggio R=5.0m con velocità costante in modulo v=64 m/s; calcolare le componenti del l'accelerazione del corpo in un sistema di riferimento la cui origine coincide con il centro della traiettoria quando il corpo si trova nel punto (5,0; 0). Disegnare qualitativamente l'andamento della componente X della velocità vx in funzione del tempo durante un periodo.
Parto con il calcolo dell'accelerazione centripeta: mi risulta 819 m/s^2. Corretto?
Il grafico mi crea problemi, io so che la velocità è un vettore costante in modulo ma variabile in direzione, vettore tangente alla traiettoria e perpendicolare al raggio. Che intendono per qualitativo? Grazie