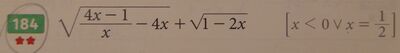√((4x-1)/x - 4x) + √(1-2x) [x<0 V x=1/2]
il sistema per trovare le condizioni d'esistenza mi viene
{4x-1-4x^2 ≥ 0
{x > 0
{1-2x ≥ 0
{x = 1/2
{x > 0
{x ≤ 1/2
ma con queste condizioni il grafico di sistema é
_________________
_________ |__________
_______|_________|__________
0 1/2
che mi dà soluzione finale: 0<x≤1/2 , che però é sbagliata
Qualcuno riesce ad aiutarmi?
189
punti
Livello 1
Ti conviene sempre studiare una disequazione fratta (alla forma normale) anziché prendere in considerazione due sistemi. Ciao Buona giornata.
@frequentante.liceo
Studiamo separatamente il campo di esistenza delle due radici. Una volta determinati gli intervalli in cui i radicandi risultano positivi o nulli, troviamo la condizione di esistenza dell'espressione INTERSECANDO (entrambe le condizioni verificate) le due precedenti condizioni.
Prima radice:
[(4x - 1 - 4x²) /x ]>=0
Il numeratore è il quadrato di un binomio ed essendo il coefficiente di grado 2 minore di zero, è sempre negativo e nullo per x=1/2.
L'intera frazione risulta quindi positiva se il denominatore è negativo, ossia x<0.
Quindi.: {x<0 v x= 1/2}
Seconda radice:
La condizione di esistenza della seconda radice è:
x<= 1/2
Dobbiamo quindi fare l'intersezione delle due soluzioni, ossia verificare in quali intervalli sono entrambe verificate.
Ciò avviene se:
x<0 v x= 1/2
75846
punti
Genius II
L'intera frazione risulta quindi positiva se x<0.
ragionando per logica capisco che se il numeratore é sempre negativo (e nullo per x = 1/2) é necessario che anche il denominatore sia negativo perché la frazione sia positiva ma non capisco come giustificarlo matematicamente
@frequentante.liceo
Il numeratore è quindi una linea sempre tratteggiata (segno meno) valore 1/2 a parte.
Il denominatore è positivo per x>0 ed è quindi una linea tratteggiata fino ad x=0 e poi linea unita da zero in avanti.
Studi il segno del quoziente e vedi che è positivo dove numeratore e denominatore hanno segno concorde ( - -)
Quindi x<0
x=1/2 va bene poiché è il valore che rende nulla l'intera frazione
@stefanopescetto ok grazie
@frequentante.liceo
Figurati. Buona giornata
Ciao.
Parti con il piede sbagliato:
{4x-1-4x^2 ≥ 0
{x > 0
{1-2x ≥ 0
Così facendo ti dimentichi che hai pure le possibilità:
{4·x - 1 - 4·x^2 ≤ 0
{x < 0
{1-2x ≥ 0
-------------------------------------
Il primo sistema ti dà soluzione:[x = 1/2]
Il secondo sistema ti dà soluzione: [x < 0]
Quindi devi avere come soluzione finale:
x < 0 ∨ x = 1/2
78174
punti
Genius II
@lucianop ah giusto, grazie per la spiegazione
La condizione di esistenza di ogni radicale, e quindi della loro somma, è: PER OGNI RADICANDO.
I radicali, in quanto potenze, sono definiti ovunque.
Quindi il loro insieme di definizione coincide col dominio.
------------------------------
Se però vuoi calcolare l'insieme di definizione reale della somma di due radicali con indice pari
* √((4*x - 1)/x - 4*x) + √(1 - 2*x)
esso consiste nella condizione composta: nessun denominatore nullo e nessun radicando negativo, cioè
* (x != 0) & ((4*x - 1)/x - 4*x >= 0) & (1 - 2*x >= 0)
Il terzo congiunto (1 - 2*x >= 0 ≡ x <= 1/2) assorbe il primo e semplifica la condizione
* ((4*x - 1)/x - 4*x >= 0) & (x <= 1/2) ≡
≡ (- (2*x - 1)^2/x >= 0) & (x <= 1/2) ≡
≡ (((2*x - 1)^2/x = 0) oppure (1/x < 0)) & (x <= 1/2) ≡
≡ ((x = 1/2) oppure (x < 0)) & (x <= 1/2) ≡
≡ (x = 1/2) & (x <= 1/2) oppure (x < 0) & (x <= 1/2) ≡
≡ (x = 1/2) oppure (x < 0)
che è proprio il risultato atteso.
52069
punti
Genius I
Se è un radicale libero direi che se la passa bene, se è al gabbio se la passa di m..da 🤭
97802
punti
Genius II
