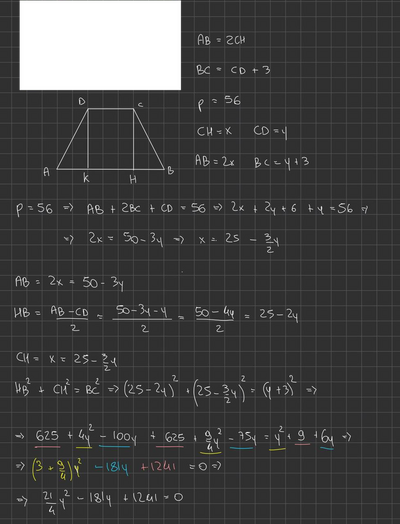
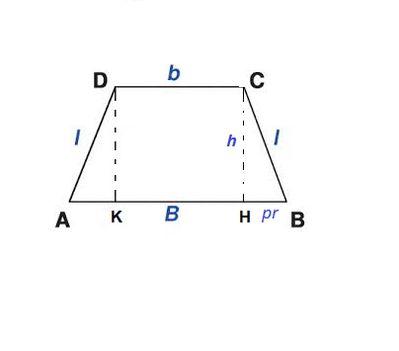
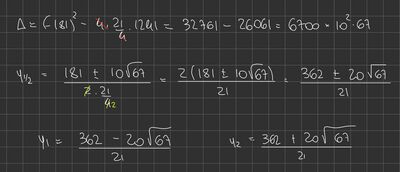Un trapezio isoscele la base maggiore doppia dell'altezza ed il lato obliquo supera di 3 dm la base minore. Calcola l'area del trapezio sapendo che il suo perimetro è di $56 \mathrm{dm}$.
Qualcuno può aiutarmi?
la risoluzione del problema è $180 \mathrm{dm}^{\wedge} 2$
I dati sono tutti
10
punti
Livello 0
Con questi dati si ottengono due possibili valori per la base minore (e quindi di conseguenza anche per base maggiore, altezza e lato obliquo) che soddisfano la condizione di avere come perimetro 56 ma in nessuno dei due casi l'area vale 180.
C'è sicuramente un errore nei dati. Se puoi postare la traccia completa dal libro sicuramente vediamo qual è l'errore che hai fatto nel trascriverla
821
punti
Livello 2
Un trapezio isoscele ABCD ha la base maggiore B doppia dell'altezza h ed il lato obliquo l supera di 3 dm la base minore. Calcola l'area del trapezio sapendo che il suo perimetro 2p è di 56 dm.
perimetro 2p = 56
56 = b+2pr+b+2(b+3)
56 = 4b+2pr+6
50 = 4b+2pr
pr = 25-2b
pr^2 = 625+4b^2-100b
l^2-h^2 = pr^2
(b+3)^2-(b+2pr)^2/4 = 625+4b^2-100 b
si mettono a sistema :
{pr = 25-2b (1)
{(b+3)^2-(b+2pr)^2/4 = pr^2 (2)
sostituisci pr nella (2) con (25-2b) e risolvi la (2) trovando b e poi pr dalla (1); B = b+2pr ; h = B/2
97875
punti
Genius II
